分类: C/C++
2010-06-18 20:33:58
那么,有什么方法可以不用比较就能排出顺序呢?借助Hash表的思想,多数人都能想出这样一种排序算法来。 我们假设给出的数字都在一定范围中,那么我们就可以开一个范围相同的数组,记录这个数字是否出现过。由于数字有可能有重复,因此Hash表的概念需要扩展,我们需要把数组类型改成整型,用来表示每个数出现的次数。 看这样一个例子,假如我们要对数列3 1 4 1 5 9 2 6 5 3 5 9进行排序。由于给定数字每一个都小于10,因此我们开一个0到9的整型数组T[i],记录每一个数出现了几次。读到一个数字x,就把对应的T[x]加一。 A[]= 3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5, 9 +---+---+---+---+---+---+---+---+---+---+ 数字 i: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | +---+---+---+---+---+---+---+---+---+---+ 出现次数T[i]: | 0 | 2 | 1 | 2 | 1 | 3 | 1 | 0 | 0 | 2 | +---+---+---+---+---+---+---+---+---+---+ 最后,我们用一个指针从前往后扫描一遍,按照次序输出0到9,每个数出现了几次就输出几个。假如给定的数是n个大小不超过m的自然数,显然这个算法的复杂度是O(m+n)的。 我曾经以为,这就是线性时间排序了。后来我发现我错了。再后来,我发现我曾犯的错误是一个普遍的错误。很多人都以为上面的这个算法就是传说中的计数排序。 问题出在哪里了?为什么它不是线性时间的排序算法?原因是,这个算法根本不是排序算法,它根本没有对原数据进行排序。 问题一:为什么说上述算法没有对数据进行排序? STOP! You should think for a while. 我们班有很多MM。和身高相差太远的MM在一起肯定很别扭,接个吻都要弯腰才行(矮 死了)。为此,我希望给我们班的MM的身高排序。我们班MM的身高,再离谱也没有超过2米的,这很适合用我们刚才的算法。我们在黑板上画一个100到 200的数组,MM依次自曝身高,我负责画“正”字统计人数。统计出来了,从小到大依次为141, 143, 143, 147, 152, 153, …。这算哪门子排序?就一排数字对我有什么用,我要知道的是哪个MM有多高。我们仅仅把元素的属性值从小到大列了出来,但我们没有对元素本身进行排序。也 就是说,我们需要知道输出结果的每个数值对应原数据的哪一个元素。下文提到的“排序算法的稳定性”也和属性值与实际元素的区别有关。 问题二:怎样将线性时间排序后的输出结果还原为原数据中的元素? STOP! You should think for a while. 同样借助Hash表的思想,我们立即想到了类似于开散列的方法。我们用链表把属性值相同的元素串起来,挂在对应的T[i]上。每次读到一个数,在增加T [i]的同时我们把这个元素放进T[i]延伸出去的链表里。这样,输出结果时我们可以方便地获得原数据中的所有属性值为i的元素。 A[]= 3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5, 9 +---+---+---+---+---+---+---+---+---+---+ 数字 i: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | +---+---+---+---+---+---+---+---+---+---+ 出现次数T[i]: | 0 | 2 | 1 | 2 | 1 | 3 | 1 | 0 | 0 | 2 | +---+o--+-o-+-o-+-o-+-o-+--o+---+---+-o-+ | | | | | | | +--+ +-+ | | +-+ +---+ | | | A[1] | | | A[6] A[2] A[7] | A[3] A[5] A[8] | | | | A[12] A[4] A[10] A[9] | A[11] 形象地说,我们在地上摆10个桶,每个桶编一个号,然后把数据分门别类放在自己所属的桶里。这种排序算法叫做桶式排序(Bucket Sort)。本文最后你将看到桶式排序的另一个用途。 链表写起来比较麻烦,一般我们不使用它。我们有更简单的方法。 问题三:同样是输出元素本身,你能想出不用链表的其它算法么? STOP! You should think for a while. A[]= 3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5, 9 +---+---+---+---+---+---+---+---+---+---+ 数字 i: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | +---+---+---+---+---+---+---+---+---+---+ 出现次数T[i]: | 0 | 2 | 1 | 2 | 1 | 3 | 1 | 0 | 0 | 2 | +---+---+---+---+---+---+---+---+---+---+ 修改后的T[i]: | 0 | 2 | 3 | 5 | 6 | 9 | 10| 10| 10| 12| +---+---+---+---+---+---+---+---+---+---+ 所有数都读入后,我们修改T[i]数组的值,使得T[i]表示数字i可能的排名的最大值。比如,1最差排名第二,3最远可以排到第五。T数组的最后一个数应该等于输入数据的数字个数。修改T数组的操作可以用一次线性的扫描累加完成。 我们还需要准备一个输出数组。然后,我们从后往前扫描A数组,依照T数组的指示依次把原数据的元素直接放到输出数组中,同时T[i]的值减一。之所以从后 往前扫描A数组,是因为这样输出结果才是稳定的。我们说一个排序算法是稳定的(Stable),当算法满足这样的性质:属性值相同的元素,排序后前后位置 不变,本来在前面的现在仍然在前面。不要觉得排序算法是否具有稳定性似乎关系不大,排序的稳定性在下文的某个问题中将变得非常重要。你可以倒回去看看前面 说的七种排序算法哪些是稳定的。 例子中,A数组最后一个数9所对应的T[9]=12,我们直接把9放在待输出序列中的第12个位置,然后T[9]变成11(这样下一次再出现9时就应该放在第11位)。 A[]= 3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5, 9 <-- T[i]= 0, 2, 3, 5, 6, 9, 10, 10, 10, 11 Ans = _ _ _ _ _ _ _ _ _ _ _ 9 接下来的几步如下: A[]= 3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5 <-- T[i]= 0, 2, 3, 5, 6, 8, 10, 10, 10, 11 Ans = _ _ _ _ _ _ _ _ 5 _ _ 9 A[]= 3, 1, 4, 1, 5, 9, 2, 6, 5, 3 <-- T[i]= 0, 2, 3, 4, 6, 8, 10, 10, 10, 11 Ans = _ _ _ _ 3 _ _ _ 5 _ _ 9 A[]= 3, 1, 4, 1, 5, 9, 2, 6, 5 <-- T[i]= 0, 2, 3, 4, 6, 7, 10, 10, 10, 11 Ans = _ _ _ _ 3 _ _ 5 5 _ _ 9 这种算法叫做计数排序(Counting Sort)。正确性和复杂度都是显然的。 问题四:给定数的数据范围大了该怎么办? STOP! You should think for a while. 前面的算法只有在数据的范围不大时才可行,如果给定的数在长整范围内的话,这个算法是不可行的,因为你开不下这么大的数组。Radix排序(Radix Sort)解决了这个难题。 昨天我没事翻了一下初中(9班)时的同学录,回忆了一下过去。我把比较感兴趣的MM的生日列在下面(绝对真实)。如果列表中的哪个MM有幸看到了这篇日志(几乎不可能),左边的Support栏有我的电子联系方式,我想知道你们怎么样了。排名不分先后。
这就是我的数据了。现在,我要给这些数排序。假如我的电脑只能开出0..99的数组,那计数排序算法最多对两位数进行排序。我就把 每个八位数两位两位地分成四段(图1),分别进行四次计数排序。地球人都知道月份相同时应该看哪一日,因此我们看月份的大小时应该事先保证日已经有序。换 句话说,我们先对“最不重要”的部分进行排序。我们先对所有数的最后两位进行一次计数排序(图2)。注意观察1月26号的MM和4月26号的MM,本次排 序中它们的属性值相同,由于计数排序是稳定的,因此4月份那个排完后依然在1月份那个的前头。接下来我们对百位和千位进行排序(图3)。你可以看到两个 26日的MM在这一次排序中分出了大小,而月份相同的MM依然保持日数有序(因为计数排序是稳定的)。最后我们对年份排序(图4),完成整个算法。大家都 是跨世纪的好儿童,因此没有图5了。 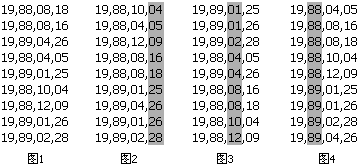 这种算法显然是正确的。它的复杂度一般写成O(d*(n+m)),其中n表示n个数,m是我开的数组大小(本例中m=100),d是一个常数因子(本例中d=4)。我们认为它也是线性的。 问题五:这样的排序方法还有什么致命的缺陷? STOP! You should think for a while. 即使数据有30位,我们也可以用d=5或6的Radix算法进行排序。但,要是给定的数据有无穷多位怎么办?有人说,这可能么。这是可能的,比如给定的数据是小数(更准确地说,实数)。基于比较的排序可以区分355/113和π哪个大,但你不知道Radix排序需要精确到哪一位。这下惨了,实数的出现把貌似高科技的线性时间排序打回了农业时代。这时,桶排序再度出山,挽救了线性时间排序悲惨的命运。 问题六:如何对实数进行线性时间排序? STOP! You should think for a while. 我们把问题简化一下,给出的所有数都是0到1之间的小数。如果不是,也可以把所有数同时除以一个大整数从而转化为这种形式。我们依然设立若干个桶,比如, 以小数点后面一位数为依据对所有数进行划分。我们仍然用链表把同一类的数串在一起,不同的是,每一个链表都是有序的。也就是说,每一次读到一个新的数都要 进行一次插入排序。看我们的例子: A[]= 0.12345, 0.111, 0.618, 0.9, 0.99999 +---+---+---+---+---+---+---+---+---+---+ 十分位: | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | +---+-o-+---+---+---+---+-o-+---+---+-o-+ | | | A[2]=0.111 A[3]=0.618 A[4]=0.9 | | A[1]=0.12345 A[5]=0.99999 假如再下一个读入的数是0.122222,这个数需要插入到十分位为1的那个链表里适当的位置。我们需要遍历该链表直到找到第一个比0.122222大的 数,在例子中则应该插入到链表中A[2]和A[1]之间。最后,我们按顺序遍历所有链表,依次输出每个链表中的每个数。 这个算法显然是正确的,但复杂度显然不是线性。事实上,这种算法最坏情况下是O(n^2)的,因为当所有数的十分位都相同时算法就是一个插入排序。和原来一样,我们下面要计算算法的平均时间复杂度,我们希望这种算法的平均复杂度是线性的。 这次算平均复杂度我们用最笨的办法。我们将算出所有可能出现的情况的总时间复杂度,除以总的情况数,得到平均的复杂度是多少。 每个数都可能属于10个桶中的一个,n个数总的情况有10^n种。这个值是我们庞大的算式的分母部分。如果一个桶里有K个元素,那么只与这个桶有关的操作 有O(K^2)次,它就是一次插入排序的操作次数。下面计算,在10^n种情况中,K0=1有多少种情况。K0=1表示,n个数中只有一个数在0号桶,其 余n-1个数的十分位就只能在1到9中选择。那么K0=1的情况有C(n,1)*9^(n-1),而每个K0=1的情况在0号桶中将产生1^2的复杂度。 类似地,Ki=p的情况数为C(n,p)*9^(n-p),复杂度总计为C(n,p)*9^(n-p)*p^2。枚举所有K的下标和p值,累加起来,这个 算式大家应该能写出来了,但是这个……怎么算啊。别怕,我们是搞计算机的,拿出点和MO不一样的东西来。于是,Mathematica 5.0隆重登场,我做数学作业全靠它。它将帮我们化简这个复杂的式子。 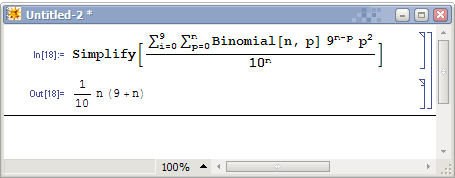 我们遗憾地发现,虽然常数因子很小(只有0.1),但算法的平均复杂度仍然是平方的。等一下,1/10的那个10是我们桶的个数吗?那么我们为什么不把桶的个数弄大点?我们干脆用m来表示桶的个数,重新计算一次: 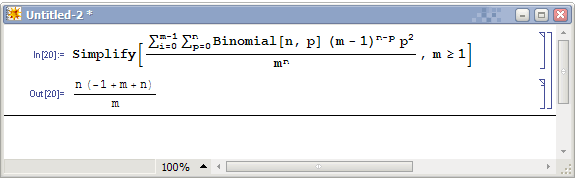 化简出来,操作次数为O(n+n^2/m)。发现了么,如果m=Θ(n)的话,平均复杂度就变成了O(n)。也就是说,当桶的个数等于输入数据的个数时,算法是平均线性的。 我们将在Hash表开散列的介绍中重新提到这个结论。 且慢,还有一个问题。10个桶以十分位的数字归类,那么n个桶用什么方法来分类呢?注意,分类的方法需要满足,一,一个数分到每个桶里的概率相同(这样才 有我们上面的结论);二,所有桶里容纳元素的范围必须是连续的。根据这两个条件,我们有办法把所有数恰好分为n类。我们的输入数据不是都在0到1之间么? 只需要看这些数乘以n的整数部分是多少就行了,读到一个数后乘以n取整得几就插入到几号桶里。这本质上相当于把区间[0,1)平均分成n份。 问题七:有没有复杂度低于线性的排序算法 STOP! You should think for a while. 我们从O(n^2)走向O(nlogn),又从O(nlogn)走向线性,每一次我们都讨论了复杂度下限的问题,根据讨论的结果提出了更优的算法。这次总 算不行了,不可能有比线性还快的算法了,因为——你读入、输出数据至少就需要线性的时间。排序算法之旅在线性时间复杂度这一站终止了,所有十种排序算法到 这里介绍完毕了。 |