本文主要讲解分类问题中的逻辑回归。逻辑回归是一个二分类问题。
二分类问题
二分类问题是指预测的y值只有两个取值（0或1），二分类问题可以扩展到多分类问题。例如：我们要做一个垃圾邮件过滤系统，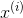
是邮件的特征，预测的y值就是邮件的类别，是垃圾邮件还是正常邮件。对于类别我们通常称为正类（positive class）和负类（negative class），垃圾邮件的例子中，正类就是正常邮件，负类就是垃圾邮件。
逻辑回归
Logistic函数
如果我们忽略二分类问题中y的取值是一个离散的取值（0或1），我们继续使用线性回归来预测y的取值。这样做会导致y的取值并不为0或1。逻辑回归使用一个函数来归一化y值，使y的取值在区间(0,1)内，这个函数称为Logistic函数(logistic function)，也称为Sigmoid函数(sigmoid function)。函数公式如下：
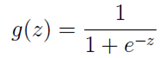
Logistic函数当z趋近于无穷大时，g(z)趋近于1；当z趋近于无穷小时，g(z)趋近于0。Logistic函数的图形如下：
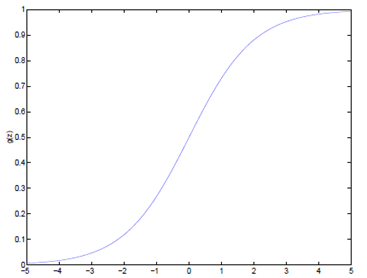
Logistic函数求导时有一个特性，这个特性将在下面的推导中用到，这个特性为：
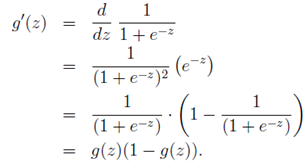
逻辑回归表达式
逻辑回归本质上是线性回归，只是在特征到结果的映射中加入了一层函数映射，即先把特征线性求和，然后使用函数g(z)将最为假设函数来预测。g(z)可以将连续值映射到0到1之间。线性回归模型的表达式带入g(z)，就得到逻辑回归的表达式:
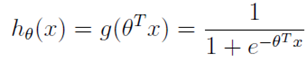
依照惯例，让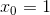
，表达式就转换为：
逻辑回归的软分类
现在我们将y的取值通过Logistic函数归一化到(0,1)间，y的取值有特殊的含义，它表示结果取1的概率，因此对于输入x分类结果为类别1和类别0的概率分别为：
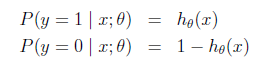
对上面的表达式合并一下就是：
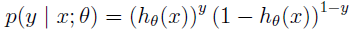
梯度上升
得到了逻辑回归的表达式，下一步跟线性回归类似，构建似然函数，然后最大似然估计，最终推导出θ的迭代更新表达式。这个思路不清楚的请参考文章《线性回归、梯度下降》，只不过这里用的不是梯度下降，而是梯度上升，因为这里是最大化似然函数不是最小化似然函数。
我们假设训练样本相互独立，那么似然函数表达式为：
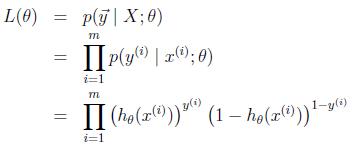
同样对似然函数取log，转换为：
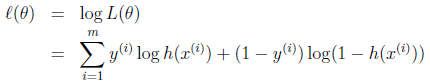
转换后的似然函数对θ求偏导，在这里我们以只有一个训练样本的情况为例：
这个求偏导过程第一步是对θ偏导的转化，依据偏导公式：y=lnx y'=1/x。
第二步是根据g(z)求导的特性g'(z) = g(z)(1 - g(z)) 。
第三步就是普通的变换。
这样我们就得到了梯度上升每次迭代的更新方向，那么θ的迭代表达式为：
这个表达式与LMS算法的表达式相比，看上去完全相同，但是梯度上升与LMS是两个不同的算法，因为表示的是关于
的一个非线性函数。
两个不同的算法，用同一个表达式表达，这并不仅仅是巧合，两者存在深层的联系。这个问题，我们将在广义线性模型GLM中解答。