从logit变换到logistic模型

https://blog.csdn.net/zengbowengood/article/details/104873012

从logit变换到logistic模型

• logit变换
• 几率
• logistic模型

前面我们知道对数函数和对数函数的一些基本性质，也许你会问，为什么要引入对数函数？而且还是一个基本初等函数？这就要从logit变换说起。

logit变换

我们在研究某一结果（y）与一系列因素$(x_1,x_2,?,x_n)$之间的关系的时候，最直白的想法是建立因变量和自变量的多元线性关系
y=α1x1+α2x2+?+αnxny=\alpha_1x_1+\alpha_2x_2+\cdots +\alpha_nx_ny=α1x1+α2x2+?+αnxn
如果结果的刻画是一个数值型的话还可以解释成某因素$x_i$变化了多少导致结果$y$也变化了多少，如果结果（y）是用来刻画结果是否（0-1）发生？或者更一般的来刻画结果（y）发生的概率（0~1）呢？这时候因素$x_i$变化导致结果（y）的变化恐怕微乎其微。实际生活中，我们知道某些关键因素会直接导致结果的发生，如亚马逊雨林一只蝴蝶翅膀偶尔振动，也许两周后就会引起美国德克萨斯州的一场龙卷风。于是，需要让线性关系发生变化，使得因素的变化，结果也会跟着发生很大变化，这时候，人们想到了logit变换

从对数函数图像来看，其在（0，1）之间的因变量的变化是很大的，也就是说自变量的变化会导致因变量的巨大变化，这就符合了微小变动带来巨大变化的效果，于是让因变量取对数，有下面式子

log(y)=α1x1+α2x2+?+αnxnlog(y)=\alpha_1x_1+\alpha_2x_2+\cdots +\alpha_nx_nlog(y)=α1x1+α2x2+?+αnxn

虽然上式解决了因变量随因素变化的敏感性问题，同时也约束了y的取值范围为$(0，+\infty )$。但是一件事情发生与否，更应该是调和对称的，也就是说一件事发生与不发生有对立性，结果可以走向必然发生（概率为1），也可以走向必然不发生（概率为0），而等式左边的取值范围不仅限于$(0，+\infty )$，于是，又引进了几率。

几率

几率（odd)是指事件发生的概率与不发生的概率之比，假设事件 A发生的概率为p，不发生的概率为1-p，那么事件A的几率为
odd(A）=p1?podd(A）=\frac{p}{1-p}odd(A）=1?pp

几率恰好反应了某一事件两个对立面，具有很好的对称性，下面我们再来看一下概率和几率的关系

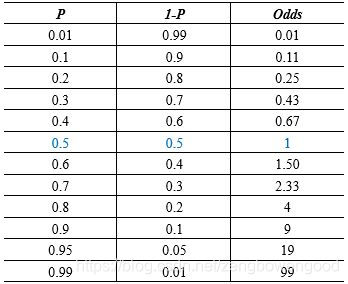
首先，我们看到概率从0.01不断增大到0.99，几率也从0.01随之不断变大到99，两者具有很好的正相关系，我们对p向两端取极限有

limp→0+(p1?p)=0\lim\limits _ {p \to 0^+}(\frac{p}{1-p})=0lim(1?pp)=0

limp→1?(p1?p)=+∞\lim\limits _ {p \to 1^-}(\frac{p}{1-p})=+\inftylim(1?pp)=+∞

于是，几率的取值范围就在$(0，+\infty )$，这符合我们之前的假设。

logistic模型

正因为概率和几率有如此密切对等的关系，于是想能不能用几率来代替概率，这样既能满足因素对结果的敏感性，又能满足对称性 ，便有了下面式子
log(p1?p)=α1x1+α2x2+?+αnxnlog(\frac{p}{1-p}) = \alpha_1x_1+\alpha_2x_2+\cdots +\alpha_nx_nlog(1?pp)=α1x1+α2x2+?+αnxn
现在，我们稍微改一改，让等式左边对数变成自然对数ln，等式右边改成向量乘积形式，便有
ln(p1?p)=αXln(\frac{p}{1-p})=\alpha Xln(1?pp)=αX
其中$\alpha =({\alpha }_1,{\alpha }_2,?,{\alpha }_n)$，$X=(x_1,x_2,?,x_n{)}^T$。
我们解得
p=eαX1+eαXp=\frac{e^{\alpha X}} {1+ e^{\alpha X}}p=1+eαXeαX
这就是我们常见的logistic模型，图像如下

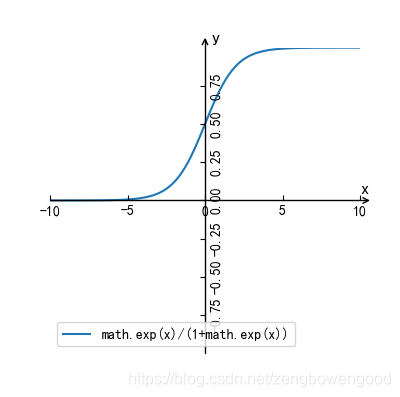
我们看到logistic函数图像是一条S型曲线，又名sigmoid曲线，以（0，0.5）为堆成中心，曲线在中心位置变化速度最快，在两端的变化速率较慢。

参考文献

1，对数函数
2，python绘制对数函数
3，如何理解logistic函数
4，logit究竟是个啥？