python实现二叉排序树

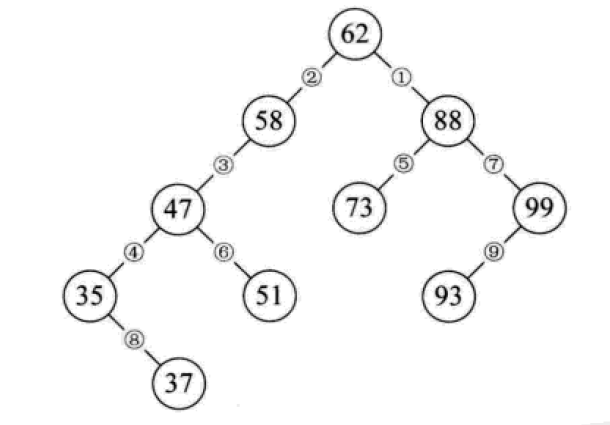
二叉排序树又称为二叉查找树。它或者是一颗空树，或者是具有下列性质的二叉树：

• 若它的左子树不为空，则左子树上所有节点的值均小于它的根结构的值；
• 若它的右子树不为空，则右子树上所有节点的值均大于它的根结构的值；
• 它的左、右子树也分别为二叉排序树。
  

• 二叉树的第i层至多有2^{i-1}个结点
• 深度为k的二叉树至多有2^k-1个结点；
• 对任何一棵二叉树T，如果其终端结点数为N0，度为2的结点数为N2，则N0=N2+1

二叉排序树的操作：

1. 查找：对比节点的值和关键字，相等则表明找到了；小了则往节点的左子树去找，大了则往右子树去找，这么递归下去，最后返回布尔值或找到的节点。
2. 插入：从根节点开始逐个与关键字进行对比，小了去左边，大了去右边，碰到子树为空的情况就将新的节点链接。
3. 删除：如果要删除的节点是叶子，直接删；如果只有左子树或只有右子树，则删除节点后，将子树链接到父节点即可；如果同时有左右子树，则可以将二叉排序树进行中序遍历，取将要被删除的节点的前驱或者后继节点替代这个被删除的节点的位置。

二叉树遍历分为三种：前序、中序、后序，其中序遍历最为重要。为啥叫这个名字？是根据根节点的顺序命名的。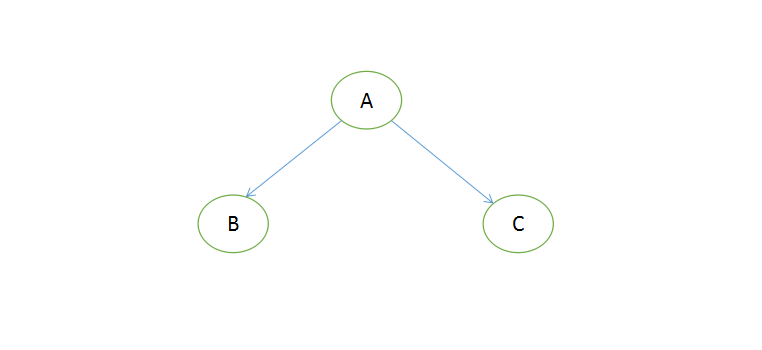

比如上图正常的一个满节点，A：根节点、B：左节点、C：右节点，前序顺序是ABC（根节点排最先，然后同级先左后右）；中序顺序是BAC(先左后根最后右）；后序顺序是BCA（先左后右最后根）。

    

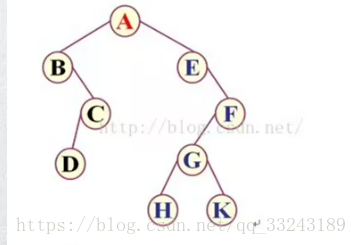
比如上图二叉树遍历结果

    前序遍历：ABCDEFGHK

    中序遍历：BDCAEHGKF

    后序遍历：DCBHKGFEA

具体代码如下：

# -*- coding:utf-8 -*-

import sys

reload(sys)
sys.setdefaultencoding('utf-8')


class BSTNode:
    """
    定义一个二叉树节点类。
    以讨论算法为主，忽略了一些诸如对数据类型进行判断的问题。
    """
    def __init__(self, data, left=None, right=None):
        """
        初始化
        :param data: 节点储存的数据
        :param left: 节点左子树
        :param right: 节点右子树
        """
        self.data = data
        self.left = left
        self.right = right


class BinarySortTree:
    """
    基于BSTNode类的二叉排序树。维护一个根节点的指针。
    """
    def __init__(self):
        self._root = None

    def is_empty(self):
        return self._root is None

    def search(self, key):
        """
        关键码检索
        :param key: 关键码
        :return: 查询节点或None
        """
        bt = self._root
        while bt:
            entry = bt.data
            if key < entry:
                bt = bt.left
            elif key > entry:
                bt = bt.right
            else:
                return entry
        return None

    def insert(self, key):
        """
        插入操作
        :param key:关键码
        :return: 布尔值
        """
        if self.is_empty():
            self._root = BSTNode(key)

        bt = self._root

        while True:
            entry = bt.data

            if key < entry:
                if bt.left is None:
                    bt.left = BSTNode(key)
                bt = bt.left
            elif key > entry:
                if bt.right is None:
                    bt.right = BSTNode(key)
                bt = bt.right
            else:
                bt.data = key
                return

    def delete(self, key):
        """
        二叉排序树最复杂的方法
        :param key: 关键码
        :return: 布尔值
        """
        p, q = None, self._root  # 维持p为q的父节点，用于后面的链接操作
        if not q:
            print("空树！")
            return
        while q and q.data != key:
            p = q
            if key < q.data:
                q = q.left
            else:
                q = q.right
            if not q: # 当树中没有关键码key时，结束退出。
                return
        # 上面已将找到了要删除的节点，用q引用。而p则是q的父节点或者None（q为根节点时）。
        if not q.left:
            if p is None:
                self._root = q.right
            elif q is p.left:
                p.left = q.right
            else:
                p.right = q.right
            return
        # 查找节点q的左子树的最右节点，将q的右子树链接为该节点的右子树
        # 该方法可能会增大树的深度，效率并不算高。可以设计其它的方法。
        r = q.left
        while r.right:
            r = r.right
        r.right = q.right
        if p is None:
            self._root = q.left
        elif p.left is q:
            p.left = q.left
        else:
            p.right = q.left

    def _pre_order(self, node=None):

        if node is None:
            node = self._root

        yield node.data

        if node.left is not None:
            for item in self._pre_order(node.left):
                yield item
        if node.right is not None:
            for item in self._pre_order(node.right):
                yield item

    def _mid_order(self, node=None):
        if node is None:
            node = self._root

        if node.left is not None:
            for item in self._mid_order(node.left):
                yield item

        yield node.data

        if node.right is not None:
            for item in self._mid_order(node.right):
                yield item

    def _mid_order1(self):
        """
        实现二叉树的中序遍历算法,
        展示我们创建的二叉排序树.
        直接使用python内置的列表作为一个栈。
        :return: data
        """
        stack = []
        node = self._root
        while node or stack:
            while node:
                stack.append(node)
                node = node.left
            node = stack.pop()
            yield node.data
            node = node.right

    def _post_order(self, node=None):
        if node is None:
            node = self._root

        if node.left is not None:
            for item in self._post_order(node.left):
                yield item

        if node.right is not None:
            for item in self._post_order(node.right):
                yield item

        yield node.data

    def pre_order(self):
        return list(self._pre_order())

    def mid_order(self):
        return list(self._mid_order()) # return list(self._mid_order1())

    def post_order(self):
        return list(self._post_order())


if __name__ == '__main__':
    lis = [62, 58, 88, 47, 73, 99, 35, 51, 93, 37]
    bs_tree = BinarySortTree()
    for i in range(len(lis)):
        bs_tree.insert(lis[i])

    print "先序遍历：", bs_tree.pre_order()
    print "中序遍历：", bs_tree.mid_order()
    print "后序遍历：", bs_tree.post_order()