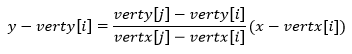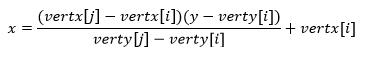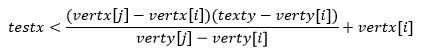PNPOLY --point inclusion in polygon

判断点在多边形内算法：

一：算法
原文网址
/> 算法核心：

I run a semi-infinite ray horizontally (increasing x, fixed y) out from the test point, and count how many edges it crosses.

（待测点为起点向右的射线，计算与多边形相交的个数，奇数个数表示点在多边形内）

源代码：
int pnpoly(int nvert, float *vertx, float *verty, float testx, float testy)

{
  int i, j, c = 0;
  for (i = 0, j = nvert-1; i < nvert; j = i++) {
    if ( ((verty[i]>testy) != (verty[j]>testy)) &&
	 (testx < (vertx[j]-vertx[i]) * (testy-verty[i]) / (verty[j]-verty[i]) + vertx[i]) )
       c = !c;
  }
  return c;
}

Argument	Meaning
nvert	Number of vertices in the polygon. Whether to repeat the first vertex at the end is discussed below.
vertx, verty	Arrays containing the x- and y-coordinates of the polygon's vertices.
testx, testy	X- and y-coordinate of the test point.

The variable c is switching from 0 to 1 and 1 to 0 each time the horizontal ray crosses any edge. So basically it's keeping track of whether the number of edges crossed are even or odd. 0 means even and 1 means odd.

二：算法一些解释
http://blog.csdn.net/hjh2005/article/details/9246967
（注：此文章中最后公式给的有错误，应是x<...）
/>

1.  最简单的方法是使用射线法，因为它能适用于所有类型的多边形，不用考虑特殊的情况而且速度也比较快。该算法的思想很简单：在多边形外面任意一点画一条虚拟的射线到p(x,y)然后计算该射线与多边形上的边相交的次数。如果该次数是偶数，说明p(x,y)在多边形外，如果是奇数，则在多边形内。

图 2

图2显示了多边形自交的情况。在这个例子中多边形的10条边有些互相交叉。这种情况很像汇编语言中的“异或”（XOR）。多边形中重叠的部分剔除。因此测试点在多边形的外面，我们从它的左右两边各有两个交点也可以看出来。

图 3

图3中多边形没有重叠，但是有两条边相交。这种情况下算法也没有问题，任然可以正常工作。

图 4

图4显示了当我们要测试的点所在的扫描行正好穿过多边形的一个顶点，因此扫描行与边a有一个交点，与边b也有一个交点，一共有两个角点，测试点的右边也是同样的情况，那按照我们的算法得到：测试点在多边形外的结论，但这显然是错误的！

要解决这种情况遇到的问题非常简单。边上的点是否与扫描行相交，我们要看边的两个端点是否是在扫描行的两侧，在扫描行上或上方的端点我们把它认为是同一种情况，那图4中边a的一个端点在扫描线的下方，另一个点在扫描线上或上方，所以边a与扫描线相交，而边b的两个端点都在扫描线上或上方，所以边b与扫描线不相交。

图 5

图5显示的多边形上一条边完全与扫描行重合的情况。根据图4中具体描述的边c的一个端点在扫描线的下方另一个端点在扫描线上或上方，所以边c与扫描线有一个交点，而边d的两个端点都在扫描线上或以上，所以无交点，边e也是两个端点都在扫描线上或以上，所以也没交点。

图 6

图6说明了一种特殊的情况（由加州州立理工大学的John David Munch指出）。多边形的一个角刚好落在扫描线上。其实这也没问题，上面的图中只有红色的边与扫描线相交产生交点，所以第一张图有1个交点第二张图有3个交点，交点的个数任然是奇数个，所以测试点在多边形内部。

2  解释  testx < (vertx[j]-vertx[i]) * (testy-verty[i]) / (verty[j]-verty[i]) + vertx[i])

直线方程




从test点发出向右发射线（y固定），与经过点vert[i]和 vert[j]直线相交，则 terstx <交点x,即下方不等式：