应roger的要求,我在此总结一下graph model。
推荐中对graph model的研究主要有两个方面,一个是如何构图,另一个是如何在图上做ranking。
关于构图问题,取决于数据,首先考虑如果我们只有user item的数据,那么最简单的方法就是构造二分图,两类节点,user节点和item节点,如果user喜欢item,就在他们中间连一条边。
如果我们有了用户的profile信息,和item的content信息,这个时候又有了很多构图的方法。一种方法是用这些信息计算出user-
user相似度和item-item相似度,然后把这些相似度作为权重,来给user节点之间,和item节点之间加边,这个称为two-layer
graph model。相关的可以参考下面两篇论文:
1. A graph-based recommender system for digital library
2. A graph model for E-commerce recommender systems
当然,如果这些额外信息比较单一,比如我们有tag信息,我们可以构造一个3分图,加入tag节点,如果一个item有某个tag,那么他们之间有 边,如果一个user用过某个tag,那么他们之间也有边。 如果是社会网络信息,我们可以直接将社会网络关系加入到user-user之间。如果我们有user参加某些group的信息,我们可以加入一类 group节点,如果一个user参加过一个group,在中间就会有一条边。
基本的构图思想就是上面这些,下面讨论图的rank问题。
图上的rank,分为三大类:
一类是基于图上的随机游走,一般用迭代法,速度很快,相关的论文有:
1.Topic-Sensitive PageRank
2.TrustWalker: a random walk model for combining trust-based and item-based recommendation
另一类是把推荐的问题看做一个半监督学习的问题,从而用传播的算法,最经典的是下面这篇博士论文
Semi-Supervised Learning with Graphs
这篇文章的作者是用图做半监督学习的权威
最好一类是用图的Laplacian矩阵来度量图中顶点的相似度,最经典的工作是下面这篇论文:
Random-Walk Computation of Similarities between Nodes of a Graph with Application to Collaborative Recommendation
上面仅仅列举了graph model中最经典的一些算法,如果深入研究这些论文,可以对graph model有个大概的认识。
http://xlvector.net/blog/?p=131
网络中顶点相似度的计算 node similarity measurement in network
Graph的一个最大好处,是他可以用尽量少的空间来存储物体(object)直接的相似度。如果我们有N个物体,要存储他们两两直接的相似度,需要用N*N的存储空间。但是用Graph可以节省很多空间,因为他可以将很多相似度隐含到网络的结构中去。
相似度图G(V,E,W).如果两个顶点直接有边连接,那么边的权重就代表两个顶点直接的相似度。那么如果两个顶点之间没有边连接呢?虽然没有边连 接,但只要图是联通的,那么肯定有若干条路径连接,这就是前面所说的,顶点的相似度蕴含在图的结构当中。那么我们的相似度函数必须在考虑图的边的同时,还 要考虑图中的路径。
以下是本文用到的一些记号
inv(A) : A的逆矩阵
pow(A,n) :A的n次方
1.Katz的方法
A new status index derived from sociometric analysis 1953
如果G的邻接矩阵是A,a(i,j)是顶点i,j的相似度。那么Katz用一下的方法来度量相似度:
S = inv(I – pA) – I = pA + pow(pA,2) + … + pow(pA,n) + …
这个方法通过邻接矩阵的n次方来考虑图中小于n的路径。这个方法的优点是定义很简单,意义也很清楚。缺点就是,矩阵的求逆计算太耗时。 而且这个方法一次性的计算了图中所有顶点对之间的相似度,如果我们仅仅要知道两个顶点直接的相似度,复杂度就太高了。
2.RandomWalk 随机游走
这个方法首先计算出
图的马尔可夫转移概率矩阵。然后在图中进行随机游走。假设从i开始随机游走,如果i,j之间有一条边,那么从i到j的转移概率是p(i,j).
那么我们考虑图中的任意一个点k,那么我们考虑如果从i出发,随机在图中游走,那么第一次走到k需要的平均步数,可以看作i,k之间的相似度。
Random-Walk
Computation of Similarities between Nodes of a Graph with Application
to Collaborative Recommendation. 2007 Francois Fouss
本文是《A Random Walk Method for Alleviating the Sparsity Problem in Collaborative Filtering》2008年的一篇论文的读书笔记
这篇论文主要贡献是提出了一种基于item-oriented 的算法,Random Walk Recommender , 第一次采用了基于item的相似度得到转移概率,并在item空间模型上进行有限步长的随机游走,来计算预测。 这种方法在训练数据上不是很丰富的情况下,效果更好。
下面是主要算法:
第1行 根据评分矩阵R来计算相似度矩阵S,R矩阵是一个n*m的矩阵,n是user数量,m是item数量;
第2-7行,生成概率转移矩阵P,系数b是一个概率,左边乘b表示有b概率的可能跳到相似的item,(1-b)的概率跳到任意一个item,跳到任意item的概率是固定的。
第8行,根据生成矩阵P生成一个新的P’,其中a是user继续访问的概率,(1-a)概率是用户直接离开,不在继续访问的概率
第9行,是根据P’和R矩阵,生成新的R矩阵,其中未知的得分将被填满。
第10行,根据R矩阵,把得分映射到1-5个分数中
最后根据得分,得出每个user的TopN推荐列表。
整个算法结束。
下面补充下由R计算S矩阵的常用方法:
第一种基本的cosine方法
测量i和j的相似度,rui是u给i的打分,S’ij 是同时给i和j打分的用户的集合。
缺点:
1.没有考虑不同用户的打分习惯,例如有的用户喜欢给他不喜欢的item打分,有点用户喜欢给他喜欢的item打分。
2. 只考虑到1个人同时给两个item打分,就增加这两个item的相似度,而实际上可能一个item1分,另一个item5分。
第二种Adjust cosine 相似度方法
同时考虑不同用户的打分习惯,也考虑到不相似和不喜欢的相似度
其中r-u是用户u打分的平均值。
测评指标:
HR(hit-rate): 就是选中的数目/实际数目
MAE(Mean Absolute Error): 惩罚实际值到真实值之间的误差
RMSE(Root Mean Square Error): 比MAE更加重了误差的惩罚
主要贡献:
这篇文章主要贡献是算法1中alpha的重要性。
- 当alpha=0时, 算法和item TOP N结果是一样的,因为TOP N算法是这个算法的一个子集, 此时Item-Item之间的相似度矩阵是比较真实准确的,这时比较符合数据集比较密集,稀疏的比较小,一般在0.6以上;
- 当alpha=1时,算法相当于忽略了user,而给予item的整体流行度进行推荐,此时数据是非常稀疏的,一般在0.2以下;
- 当alpha在0到1之间时,是比较好的,相当于在有限步长中进行推荐,步长一般在2-10之间,此时的数据集是适中的,一般在0.2-0.6之间;
该算法在数据比较稀疏时也能比较好推荐,这是该算法的主要贡献。
搜索引擎的检索结果页下方一般会提示多个相似的搜索关键词,这些词可以被看作查询关键词query的rewriting。在计算广告中,当某一个 query没有对应的bid phase出价广告,或者该query对应的bid phase较少的时候,可以利用query rewriting获取相似query对应的广告进行显示,以期望获得更多的click。相似query的确定可以利用用户session中的搜索关键词 上下文,但此方法需要确定query的边界,例如用户搜索过程中可能会突然跳到一个完全不相干的搜索,然后又跳回来。或者利用传统的文本相似度匹配,而由 于query一般都很短,传统相似度匹配的语料也不足。
Simrank
Simrank算法是一种用于衡量结构上下文中个体相似度的方法,直观上的含义是利用已有个体的相似度来推算其他与有关联个体的相似度。形式化的定义如下:
有向图G={V,E}中,节点a的入边集合记为I(a),而出边集合记为O(a),则两个节点a,b(a != b时)相似度s(a,b)按照如下公式计算,其含义是个体a,b的相似度取决于所有与a,b相连节点的相似度,s(a,b)∈[0,1];当a=b 时,s(a,b)=1;如果a != b,且只有同一个入节点c,我们不希望从c计算得到的s(a,b)也为1,因此c做为衰减因子,取值是[0,1],即s(a,b) = C。
对于二分图G’ = (V1,V2,E),对于任意的(A,a)∈E,有A∈V1和a∈V2,则所有V1集合中的节点相似度按照出度O(A)计算。V2集合中的节点相似度则按照上述公式,利用入度I(a)计算。
在搜索广告中,把query和ad看作节点,当用户搜索某个查询关键词q时,点击了广告a,则建立q至a的一条边,这样构成一个由query和ad 组成的二分图G=(V,E),其中V=Vq∪Va,任何边e=(q,a,w),q∈Vq并且a∈Va,可以利用simrank算法来求query之间的相 似度。E(q)表示q的边,N(q)表示E(q)的个数:
按照上述算法,我们看以下的例子,假设C等于0.8,则利用上述公式计算出的sim(pc,camera)的相似度在前5次迭代中都大于 sim(camera,digital camera),但从直观上说,由于camera和digital camera的共同邻居较多,应该具备更高的相似度,而simrank的结果是反直观的。针对上述问题,Antonellis等人在VLDB 08上提出了Simrank在计算广告方面的改进——Simrank++。
Simrank++
Simrank++的改进主要包括两点,一是针对上面的问题对sim(q,q`)进行调整,如果两个节点共同节点{E(q)∩E(q`)}越多,则给予这两个节点相似度更高的权值。
按照上述调整后,上面示例的计算结果如下。同时Antonellis等人也证明了,如果迭代的次数足够多,对于未调整前的simrank,最终 sim(pc,camera)会和sim(camera, digital camera)相等,但实际使用中肯定无法计算那么多次迭代。
另外一个改进就是对Simrank中的边进行加权,权值的常用设定方式包括query和ad的对应的显示次数、点击次数以及点击率CTR等。但具体 也需要考量,采用显示次数作为权值会显得用户反馈不足,可信度不够;采用点击次数,即使query和ad的关联性不强,则显示次数多的被点击次数也多;而 CTR则会受广告显示位置的影响,关联度不高但位置第一的ad获得的CTR也可能相对较高,并且对于相同的CTR,显示次数为10次和10000次 时,CTR的可信度也不同。
例如,对于上图的两种情况,如果不考虑边的权值,即使加上evidence调整,sim(flower,orchids)的计算结果也是一样的。但 直观上可以看出左边的相似度应该高于右边的相似度,Antonellis等人给出了以下方法,按照节点所有边的权值方差进行相似度调整,并对权值均一化。
定义W(a)为所有与a相邻边的权值组成的集合,即{w(i,a),w(j,a)….w(n,a)},variance(a)则为W(a)的方差,计算如下
由Simrank计算的图中两个节点的相似度,也可以用Random Walk模型来解释,即两个节点a,b的相似度可以认为是同时从a,b节点出发,随机选择下一步的邻接点,直到相遇在某一点的期望距离(Expected Meeting Distance),期望距离越短则相似度越高。
按照Simrank的原理,感觉Simrank有点类似PageRank的思想,都是利用邻居节点来进行估算。Simrank算法应该也可以用于在推荐系统中计算person,item的相似度从而进行推荐。
参考资料:
Spectral Clustering
Spectral Clustering(谱聚类)是一种基于图论的聚类方法,它能够识别任意形状的样本空间且收敛于全局最有解,其基本思想是利用样本数据的相似矩阵进行特征分解后得到的特征向量进行聚类,可见,它与样本feature无关而只与样本个数有关。
一、图的划分
图划分的目的是将有权无向图划分为两个或以上子图,使得子图规模差不多而割边权重之和最小。图的划分可以看做是有约束的最优化问题,它的目的是看怎么把每个点划分到某个子图中,比较不幸的是当你选择各种目标函数后发现该优化问题往往是NP-hard的。
怎么解决这个问题呢?松弛方法往往是一种利器(比如SVM中的松弛变量),对于图的划分可以认为能够将某个点的一部分划分在子图1中,另一部分划分在子图 2中,而不是非此即彼,使用松弛方法的目的是将组合优化问题转化为数值优化问题,从而可以在多项式时间内解决之,最后在还原划分时可以通过阈值来还原,或 者使用类似K-Means这样的方法,之后会有相关说明。
二、相关定义
1、用表示无向图,其中
和
分别为其顶点集和边集;
2、说某条边属于某个子图是指该边的两个顶点都包含在子图中;
3、假设边的两个不同端点为
和
,则该边的权重用
表示,对于无向无环图有
且
,为方便以下的“图”都指无向无环图;
4、对于图的某种划分方案的定义为:所有两端点不在同一子图中的边的权重之和,它可以被看成该划分方案的损失函数,希望这种损失越小越好,本文以二分无向图为例,假设原无向图
被划分为
和
,那么有:
三、Laplacian矩阵
假设无向图被划分为
和
两个子图,该图的顶点数为:
,用
表示
维指示向量,表明该划分方案,每个分量定义如下:
于是有:
又因为:
其中,为对角矩阵,对角线元素为:
为权重矩阵:
且
。
重新定义一个对称矩阵,它便是Laplacian矩阵:
矩阵元素为:
如果所有权重值都为非负,那么就有,这说明Laplacian矩阵
是半正定矩阵;而当无向图为连通图时
有特征值0且对应特征向量为
,这反映了,如果将无向图
划分成两个子图,一个为其本身,另一个为空时,
为0(当然,这种划分是没有意义的)。
这个等式的核心价值在于:将最小化划分的问题转变为最小化二次函数
;从另一个角度看,实际上是把原来求离散值松弛为求连续实数值。
观察下图:
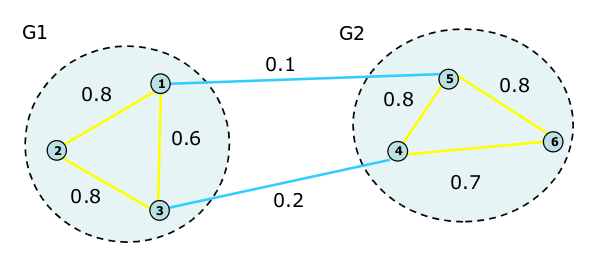
图1
它所对应的矩阵为:
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 0.0 0.8 0.6 0.0 0.1 0.0
[2,] 0.8 0.0 0.8 0.0 0.0 0.0
[3,] 0.6 0.8 0.0 0.2 0.0 0.0
[4,] 0.0 0.0 0.2 0.0 0.8 0.7
[5,] 0.1 0.0 0.0 0.8 0.0 0.8
[6,] 0.0 0.0 0.0 0.7 0.8 0.0
 矩阵为:
矩阵为:
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 1.5 0.0 0.0 0.0 0.0 0.0
[2,] 0.0 1.6 0.0 0.0 0.0 0.0
[3,] 0.0 0.0 1.6 0.0 0.0 0.0
[4,] 0.0 0.0 0.0 1.7 0.0 0.0
[5,] 0.0 0.0 0.0 0.0 1.7 0.0
[6,] 0.0 0.0 0.0 0.0 0.0 1.5
Laplacian矩阵为:
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 1.5 -0.8 -0.6 0.0 -0.1 0.0
[2,] -0.8 1.6 -0.8 0.0 0.0 0.0
[3,] -0.6 -0.8 1.6 -0.2 0.0 0.0
[4,] 0.0 0.0 -0.2 1.7 -0.8 -0.7
[5,] -0.1 0.0 0.0 -0.8 1.7 -0.8
[6,] 0.0 0.0 0.0 -0.7 -0.8 1.5
Laplacian矩阵是一种有效表示图的方式,任何一个Laplacian矩阵都对应一个权重非负地无向有权图,而满足以下条件的就是Laplacian矩阵:
1、 为对称半正定矩阵,保证所有特征值都大于等于0;
为对称半正定矩阵,保证所有特征值都大于等于0;
2、 矩阵有唯一的0特征值,其对应的特征向量为
矩阵有唯一的0特征值,其对应的特征向量为 ,它反映了图的一种划分方式:一个子图包含原图所有端点,另一个子图为空。
,它反映了图的一种划分方式:一个子图包含原图所有端点,另一个子图为空。
四、划分方法
1、Minimum Cut 方法
考虑最简单情况,另,无向图划分指示向量定义为:
要优化的目标为,由之前的推导可以将该问题松弛为以下问题:
从这个问题的形式可以联想到Rayleigh quotient:
原问题的最优解就是该Rayleigh quotient的最优解,而由Rayleigh quotient的性质可知:它的最小值,第二小值,......,最大值分别对应矩阵的最小特征值,第二小特征值,......,最大特征值,且极值
在相应的特征向量处取得,即需要求解下特征系统的特征值和特征向量:
这里需要注意约束条件,显然
的最小特征值为0,此时对应特征向量为
,不满足这个约束条件(剔除了无意义划分),于是最优解应该在第二小特征值对应的特征向量处取得。
当然,求得特征向量后还要考虑如何恢复划分,比如可以这样:特征向量分量值为正所对应的端点划分为,反之划分为
;也可以这样:将特征向量分量值从小到大排列,以中位数为界划分
和
;还可以用K-Means算法聚类。
2、Ratio Cut 方法
实际当中,划分图时除了要考虑最小化外还要考虑划分的平衡性,为缓解出现类似一个子图包含非常多端点而另一个只包含很少端点的情况,出现了Ratio Cut,它衡量子图大小的标准是子图包含的端点个数。
定义为子图1包含端点数,
为子图2包含端点数,
,则优化目标函数为:
其中:
做一个简单变换:
其中:
看吧,这形式多给力,原问题就松弛为下面这个问题了:
依然用Rayleigh quotient求解其第二小特征值及其特征向量。
3、Normalized Cut 方法
与Ratio Cut类似,不同之处是,它衡量子图大小的标准是:子图各个端点的Degree之和。
定义:为子图1Degree之和:
为子图2Degree之和:
则优化目标函数为:
其中:
原问题就松弛为下面这个问题了:
用泛化的Rayleigh quotient表示为:
那问题就变成求解下特征系统的特征值和特征向量:
——式子1
(注:
是一个对角矩阵,且
)
(其中:
,
) ——式子2
显然,式子1和式子2有相同的特征值,但是对应特征值的特征向量关系为:,因此我们可以先求式子2的特征值及其特征向量,然后为每个特征向量乘以
就得到式子1的特征向量。
哦,对了,矩阵叫做Normalized Laplacian,因为它对角线元素值都为1。
五、Spectral Clustering

1、Unnormalized Spectral Clustering算法
2、Normalized Spectral Clustering算法
3、以图1为例,取K=2,使用Unnormalized Spectral Clustering算法,此时聚类的对象其实就是矩阵L的第二小特征向量(使用R模拟):
● L矩阵为:
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 1.5 -0.8 -0.6 0.0 -0.1 0.0
[2,] -0.8 1.6 -0.8 0.0 0.0 0.0
[3,] -0.6 -0.8 1.6 -0.2 0.0 0.0
[4,] 0.0 0.0 -0.2 1.7 -0.8 -0.7
[5,] -0.1 0.0 0.0 -0.8 1.7 -0.8
[6,] 0.0 0.0 0.0 -0.7 -0.8 1.5
● q<-eigen(L) 求得L的特征值和特征向量分别为:
$values
[1] 2.573487e+00 2.469025e+00 2.285298e+00 2.084006e+00 1.881842e-01 1.776357e-15
$vectors
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] -0.10598786 -0.3788245748 -0.30546656 0.64690880 0.4084006 -0.4082483
[2,] -0.21517718 0.7063206485 0.30450981 -0.01441501 0.4418249 -0.4082483
[3,] 0.36782805 -0.3884382495 0.04461661 -0.63818761 0.3713186 -0.4082483
[4,] -0.61170644 -0.0009962363 -0.45451793 -0.33863293 -0.3713338 -0.4082483
[5,] 0.65221488 0.3509689196 -0.30495543 0.16645901 -0.4050475 -0.4082483
[6,] -0.08717145 -0.2890305075 0.71581349 0.17786774 -0.4451628 -0.4082483
● q$vectors[,5] 取第二小特征向量:
[1] 0.4084006 0.4418249 0.3713186 -0.3713338 -0.4050475 -0.4451628
● kmeans(q$vectors[,5],2) 利用K-Means算法聚类:
K-means clustering with 2 clusters of sizes 3, 3
Cluster means:
[,1]
1 -0.4071814
2 0.4071814
Clustering vector:
[1] 2 2 2 1 1 1
Within cluster sum of squares by cluster:
[1] 0.002732195 0.002487796
(between_SS / total_SS = 99.5 %)
http://www.cnblogs.com/vivounicorn/archive/2012/02/10/2343377.html
从结果上可以看到顶点1、2、3被聚为一类,顶点4、5、6被聚为一类,与实际情况相符。
在Mahout中已经有相应实现,放在下次学习吧。
六、总结
1、图划分问题中的关键点在于选择合适的指示向量并将其进行松弛化处理,从而将最小化划分
的问题转变为最小化二次函数
,进而转化为求Rayleigh quotient极值的问题;
2、 Spectral Clustering的各个阶段为:
● 选择合适的相似性函数计算相似度矩阵;
●计算矩阵L的特征值及其特征向量,比如可以用Lanczos迭代算法;
●如何选择K,可以采用启发式方法,比如,发现第1到m的特征值都挺小的,到了m+1突然变成较大的数,那么就可以选择K=m;
● 使用K-Means算法聚类,当然它不是唯一选择;
● Normalized Spectral Clustering在让Cluster间相似度最小而Cluster内部相似度最大方面表现要更好,所以首选这类方法。
六、参考资料
1、Chris Ding.《A Tutorial on Spectral Clustering》、《Data Mining using Matrix and Graphs》
2、Jonathan Richard Shewchuk. 《Spectral and Isoperimetric Graph Partitioning》
3、Denis Hamad、Philippe Biela.《Introduction to spectral clustering》
4、Francis R. Bach、Michael I. Jordan.《Learning Spectral Clustering》
5、丕子.
















