C++,python,热爱算法和机器学习
全部博文（1214）
分类： Python/Ruby
2021-04-27 16:47:02
-o---T
# T 就是宝藏的位置, o 是探索者的位置
这一次我们会用 q-learning 的方法实现一个小例子，例子的环境是一个一维世界，在世界的右边有宝藏，探索者只要得到宝藏尝到了甜头，然后以后就记住了得到宝藏的方法，这就是他用强化学习所学习到的行为。
Q-learning 是一种记录行为值 (Q value) 的方法，每种在一定状态的行为都会有一个值 Q(s, a)，就是说 行为 a 在 s 状态的值是 Q(s, a)。s 在上面的探索者游戏中，就是 o 所在的地点了。而每一个地点探索者都能做出两个行为 left/right，这就是探索者的所有可行的 a 啦。
致谢：上面三段文字来自这里：
要解决这个问题，下面的几个事情要先搞清楚：
epsilon = 0.9 # 贪婪度 greedy alpha = 0.1 # 学习率 gamma = 0.8 # 奖励递减值
探索者的状态，即其可到达的位置，有6个。所以定义
states = range(6) # 状态集，从0到5
那么，在某个状态下执行某个动作之后，到达的下一个状态如何确定呢？
def get_next_state(state, action): '''对状态执行动作后，得到下一状态''' global states # left, right = -1,+1 # 一般来说是这样，不过要考虑首尾两个位置 if action == 'right' and state != states[-1]: # 除最后一个状态（位置），皆可向右(+1) next_state = state + 1 elif action == 'left' and state != states[0]: # 除最前一个状态（位置），皆可向左(-1) next_state = state -1 else: next_state = state return next_state
探索者处于每个状态时，可行的动作，只有"左"或"右"2个。所以定义
actions = ['left', 'right'] # 动作集。也可添加动作'none'，表示停留
那么，在某个给定的状态（位置），其所有的合法动作如何确定呢？
def get_valid_actions(state): '''取当前状态下的合法动作集合，与rewards无关！''' global actions # ['left', 'right'] valid_actions = set(actions) if state == states[-1]: # 最后一个状态（位置），则 valid_actions -= set(['right']) # 去掉向右的动作 if state == states[0]: # 最前一个状态（位置），则 valid_actions -= set(['left']) # 去掉向左 return list(valid_actions)
探索者到达每个状态（位置）时，要有奖励。所以定义
rewards = [0,0,0,0,0,1] # 奖励集。只有最后的宝藏所在位置才有奖励1，其他皆为0
显然，取得状态state下的奖励就很简单了：rewards[state] 。根据state，按图索骥即可，无需额外定义一个函数。
最重要。Q table是一种记录状态-行为值 (Q value) 的表。常见的q-table都是二维的，基本长下面这样：
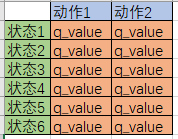（注意，也有3维的Q table）
所以定义
q_table = pd.DataFrame(data=[[0 for _ in actions] for _ in states], index=states, columns=actions)
考虑环境的目的，是让人们能通过屏幕观察到探索者的探索过程，仅此而已。
环境环境很简单，就是一串字符 '-----T'！探索者到达状态（位置）时，将该位置的字符替换成'o'即可，最后重新打印整个字符串！所以
def update_env(state): '''更新环境，并打印''' global states env = list('-----T') if state != states[-1]: env[state] = 'o' print('\r{}'.format(''.join(env)), end='') time.sleep(0.1)
Q-learning算法的伪代码
中文版的伪代码：
图片来源：
Q value的更新是根据贝尔曼方程：
好吧，是时候实现它了：
# 总共探索13次 for i in range(13): # 0.从最左边的位置开始（不是必要的） current_state = 0 #current_state = random.choice(states) # 亦可随机 while current_state != states[-1]: # 1.取当前状态下的合法动作中，随机（或贪婪）地选一个作为 当前动作 if (random.uniform(0,1) > epsilon) or ((q_table.ix[current_state] == 0).all()): # 探索 current_action = random.choice(get_valid_actions(current_state)) else: current_action = q_table.ix[current_state].idxmax() # 利用（贪婪） # 2.执行当前动作，得到下一个状态（位置） next_state = get_next_state(current_state, current_action) # 3.取下一个状态所有的Q value，待取其最大值 next_state_q_values = q_table.ix[next_state, get_valid_actions(next_state)] # 4.根据贝尔曼方程，更新 Q table 中当前状态-动作对应的 Q value q_table.ix[current_state, current_action] += alpha * (rewards[next_state] + gamma * next_state_q_values.max() - q_table.ix[current_state, current_action]) # 5.进入下一个状态（位置） current_state = next_state print('\nq_table:') print(q_table)
好了，这就是大名鼎鼎的Q-learning算法！
注意，贝尔曼方程中，取奖励是用了 rewards[next_state]，再强调一下：next_state
当然，我们希望能看到探索者的探索过程，那就随时更新（打印）环境即可：
for i in range(13): #current_state = random.choice(states) current_state = 0 update_env(current_state) # 环境相关 total_steps = 0 # 环境相关 while current_state != states[-1]: if (random.uniform(0,1) > epsilon) or ((q_table.ix[current_state] == 0).all()): # 探索 current_action = random.choice(get_valid_actions(current_state)) else: current_action = q_table.ix[current_state].idxmax() # 利用（贪婪） next_state = get_next_state(current_state, current_action) next_state_q_values = q_table.ix[next_state, get_valid_actions(next_state)] q_table.ix[current_state, current_action] += alpha * (reward[next_state] + gamma * next_state_q_values.max() - q_table.ix[current_state, current_action]) current_state = next_state update_env(current_state) # 环境相关 total_steps += 1 # 环境相关 print('\rEpisode {}: total_steps = {}'.format(i, total_steps), end='') # 环境相关 time.sleep(1) # 环境相关 print('\r ', end='') # 环境相关 print('\nq_table:') print(q_table)
