KDD 2019论文解读：多分类下的模型可解释性

日前，由阿里巴巴研究型实习生张雪舟、蚂蚁金服高级算法专家娄寅撰写的论文《Axiomatic Interpretability for Multiclass Additive Models》入选全球数据挖掘顶级会议KDD 2019，本文为该论文的详细解读。论文地址：

前言

模型可解释性是机器学习研究中的一个重要课题。这里我们研究的对象是广义加性模型（Generalized Additive Models，简称GAMs）。GAM在医疗等对解释性要求较高的场景下已经有了广泛的应用 [1]。

GAM作为一个完全白盒化的模型提供了比（广义）线性模型（GLMs）更好的模型表达能力：GAM能对单特征和双特征交叉（pairwise interaction）做非线性的变换。带pairwiseinteraction的GAM往往被称为GA2M。以下是GA2

M模型的数学表达：

其中g是linkfunction，fi和fij被称为shape function，分别为模型所需要学习的特征变换函数。由于fi和fij都是低纬度的函数，模型中每一个函数都可以被可视化出来，从而方便建模人员了解每个特征是如何影响最终预测的。例如在[1]中，年龄对肺炎致死率的影响就可以用一张图来表示。

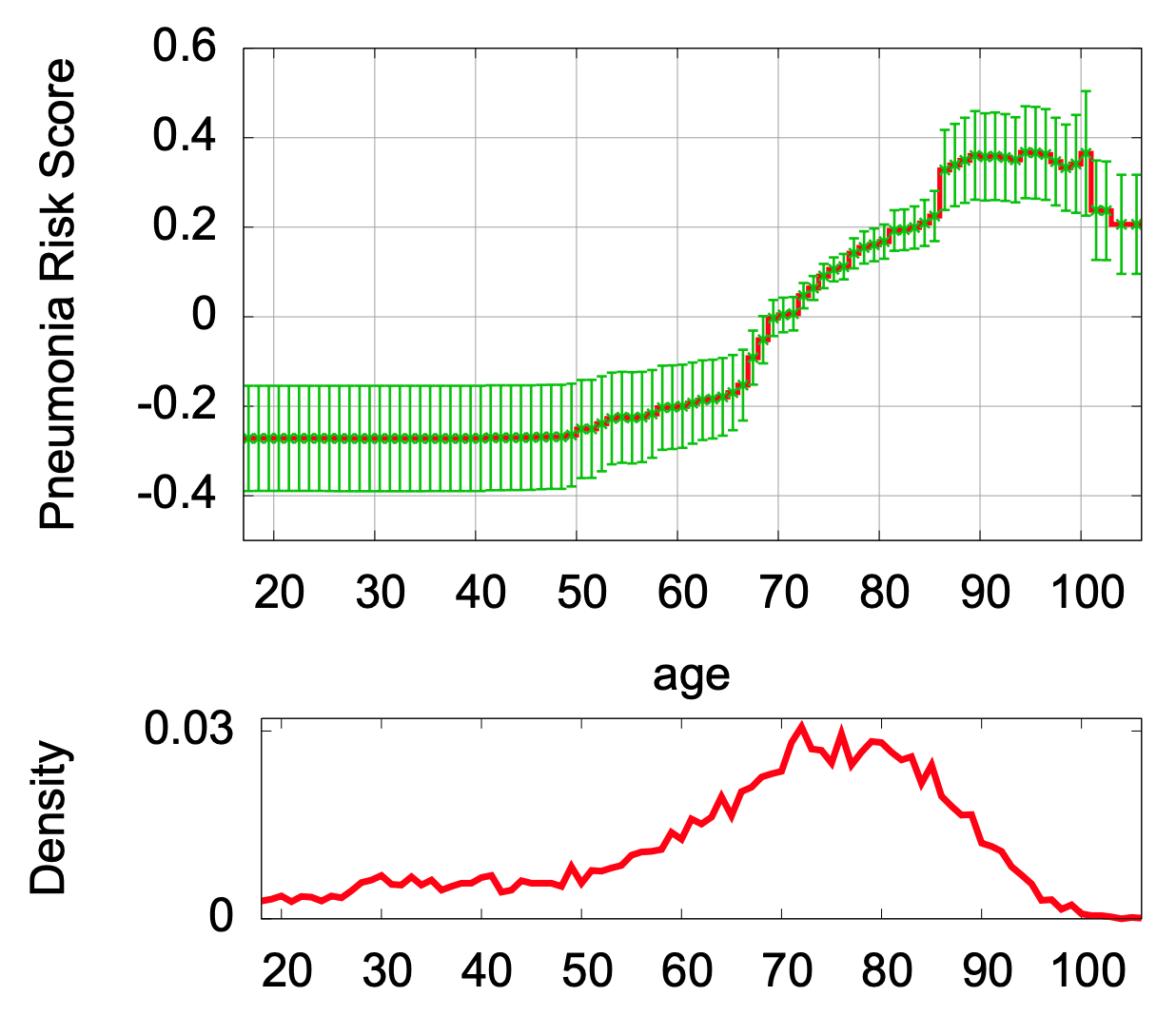
由于GAM对特征做了非线性变换，这使得GAM往往能提供比线性模型更强大的建模能力。在一些研究中GAM的效果往往能逼近Boosted Trees或者Random Forests [1, 2, 3]。

可视化图像与模型的预测机制之间的矛盾

本文首先讨论了在多分类问题的下，传统可解释性算法（例如逻辑回归，SVM）的可视化图像与模型的预测机制之间存在的矛盾。如果直接通过这些未经加工的可视化图像理解模型预测机制，有可能造成建模人员对模型预测机制的错误解读。如图1所示，左边是在一个多分类GAM下age的shape function。粗看之下这张图表示了Diabetes I的风险随年龄增长而增加。然而当我们看实际的预测概率（右图），Diabetes I的风险其实应该是随着年龄的增加而降低的。

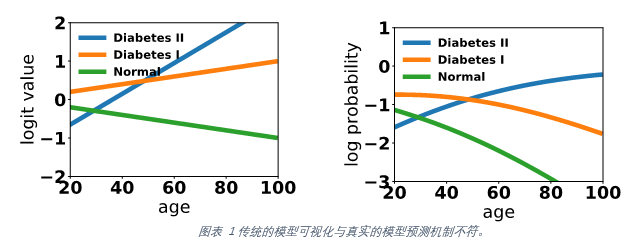
为了解决这一问题，本文提出了一种后期处理方法（AdditivePost-Processing for Interpretability, API），能够对用任意算法训练的GAM进行处理，使得在不改变模型预测的前提下，处理后模型的可视化图像与模型的预测机制相符，由此让建模人员可以安全的通过传统的可视化方法来观察和理解模型的预测机制，而不会被错误的视觉信息误导。

多分类下的模型可解释性

API的设计理念来源于两个在长期使用GAM的过程中得到的可解释性定理（Axioms of Interpretability）。我们希望一个GAM模型具备如下两个性质：

1. 任意一个shape function fik (对应feature i和class k)的形状，必须要和真实的预测概率Pk的形状相符，即我们不希望看到一个shape function是递增的，但实际上预测概率是递减的情况。

1. Shape function应该避免任何不必要的不平滑。不平滑的shape function会让建模人员难以理解模型的预测趋势。

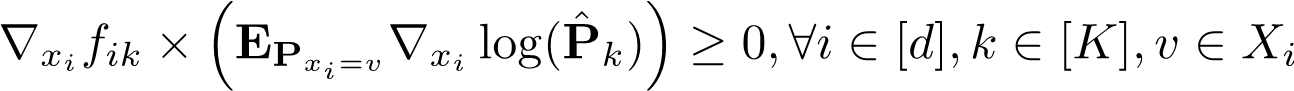
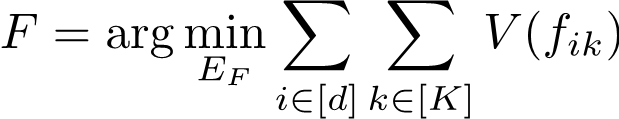
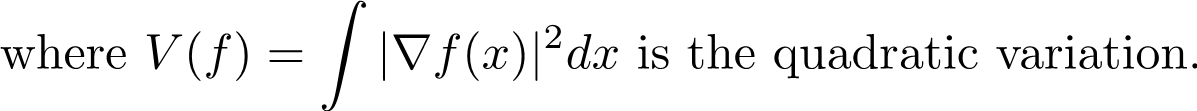
现在我们知道我们想要的模型需要满足什么性质，那么如何找到这样的模型，而不改变原模型的预测呢？这里就要用到一个重要的softmax函数的性质。

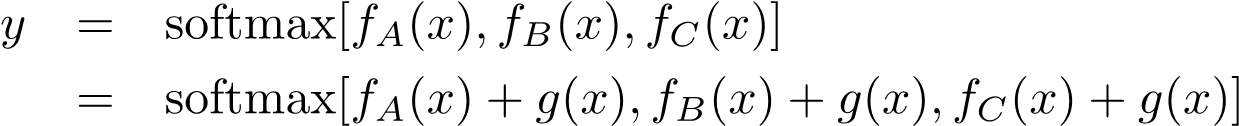
对于一个softmax函数，如果在每一个输入项中加上同一个函数，由此得来的模型是和原模型完全等价的。也就是说，这两个模型在任何情况下的预测结果都相同。基于这样的性质，我们就可以设计一个g 函数，让加入g函数之后的模型满足我们想要的性质。

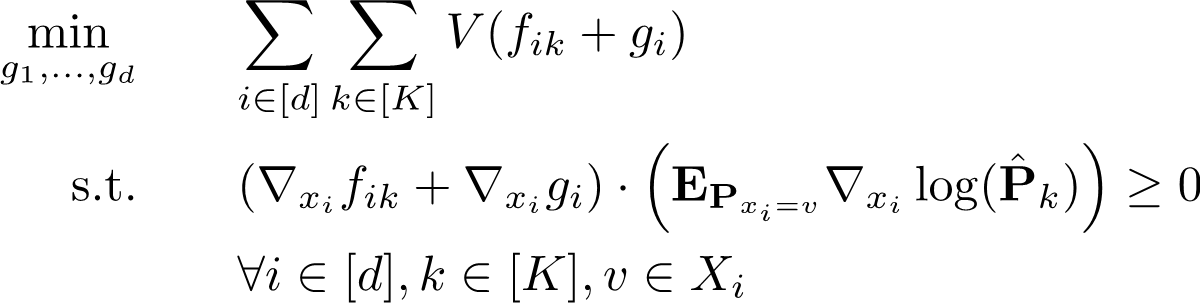
我们在文章中从数学上证明，以上这个优化问题永远有唯一的全局最优解，并且我们给出了这个解的解析形式。我们基于此设计的后期处理方法几乎不消耗任何计算资源，却可以把具有误导性的GAM模型转化成可以放心观察的可解释模型。

在一个预测婴儿死因的数据上（12类分类问题），我们采用API对shapefunction做了处理，从而使得他们能真实地反应预测概率变化的趋势。这里可以看到，在采用API之前，模型可视化提供的信息是所有死因都和婴儿体重和Apgar值成负相关趋势。但是在采用API之后我们发现，实际上不同的死因与婴儿体重和Apgar值的关系

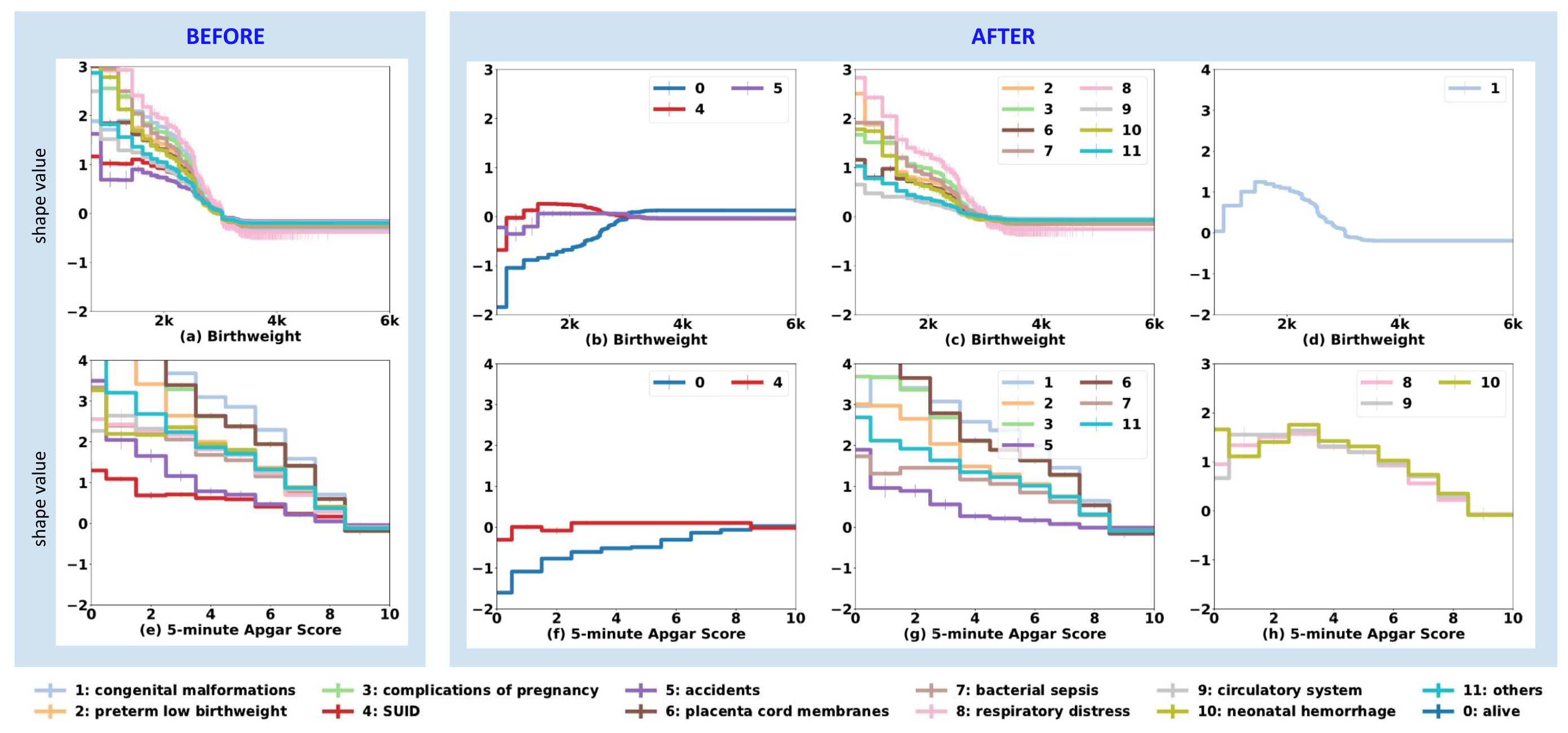
是不一样的：其中一些死因是正相关，一些死因是负相关，另外一些在婴儿体重和Apgar值达到某个中间值得时候死亡率达到最高。API使得医疗人员能够通过模型得到更准确的预测信息。

总结

在很多mission-critical的场景下（医疗，金融等），模型可解释性往往比模型自身的准确性更重要。广义加性模型作为一个高精确度又完全白盒化的模型，预期能在更多的应用场景上落地。

Reference

[1] Caruana et al. Intelligible Modelsfor HealthCare: Predicting Pneumonia Risk and Hospital 30-day Readmission. In KDD2015.

[2] Lou et al. Intelligible Models for Classification and Regression. In KDD2012.

[3] Lou et al. Accurate Intelligible Models withPairwise Interactions. In KDD 2013.