机器算法学习-随机森林算法

1.随机森林算法简介

在机器学习中通常分为有监督学习、无监督学习，半监督学习和强化学习四大类。而随机森林是一种典型的有监督学习算法，它是在决策树基础上得到的一种集成学习（bagging）算法。

随机森林，顾名思义就是由多棵决策树组成的一种算法（这里可以回想一下上节课讲的决策树算法的实现过程），同样既可以作为分类模型，也可以作为回归模型。在现实中更常用作分类模型，当然它也可以作为一种特征选择方法。而“随机”主要指两个方面：{BANNED}中国第一，随机选样本，即从原始数据集中进行有放回的抽样，得到子数据集，子数据集样本量保持与原始数据集一致，不同子数据集间的元素可以重复，同一个子数据集间的元素也可以重复。第二，随机选特征，与随机选样本过程类似，子数据集从所有原始待选择的特征中选取一定数量的特征子集，然后从再已选择的特征子集中选择{BANNED}最佳优特征的过程。通过每次选择的数据子集和特征子集来构成决策树，{BANNED}最佳终得到随机森林算法。

2.随机算法生成过程

<1 从原始数据集中每次随机有放回抽样选取与原始数据集相同数量的样本数据，构造数据子集；

<2 每个数据子集从所有待选择的特征中随机选取一定数量的{BANNED}最佳优特征作为决策树的输入特征；

<3 根据每个数据子集分别得到每棵决策树，由多棵决策树共同组成随机森林；

<4 {BANNED}最佳后如果是分类问题，则按照投票的方式选取票数{BANNED}最佳多的类作为结果返回，如果是回归问题，则按照平均法选取所有决策树预测的平均值作为结果返回。

3.想要了解随机森林算法，需要先了解集成学习的模型

集成学习通过训练学习出多个估计器，当需要预测时通过结合器将多个估计器的结果整合起来当作{BANNED}最佳后的结果输出。（如下图为集成学习的基本流程）


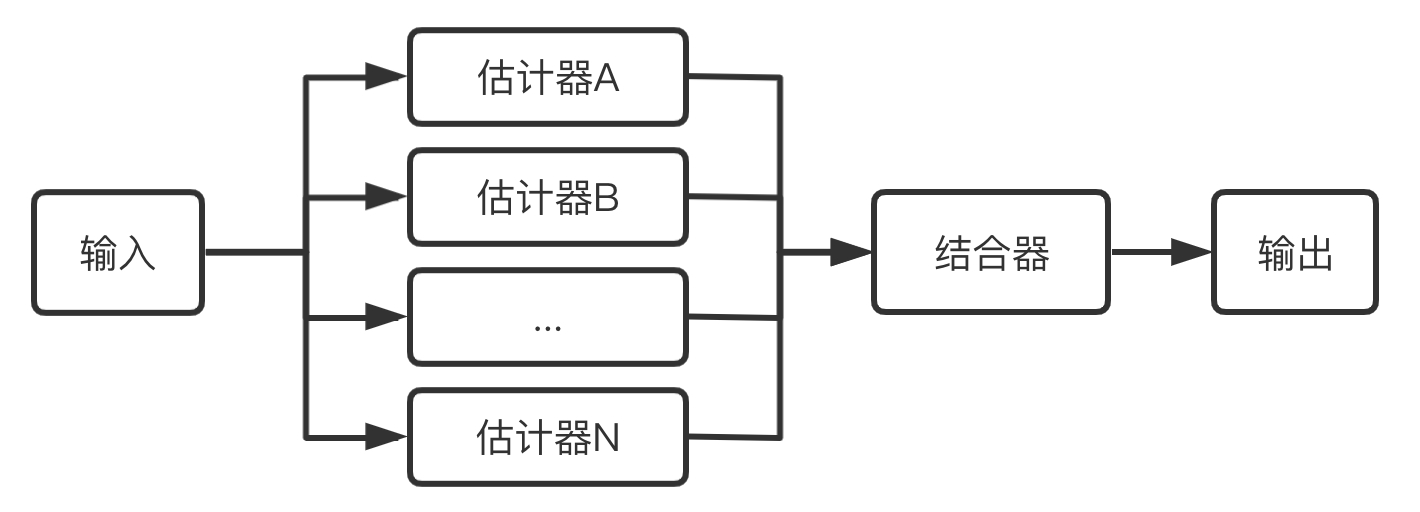   集成学习的优势是提升了单个估计器的通用性与鲁棒性，比单个估计器拥有更好的预测性能。集成学习的另一个特点是能方便的进行并行化操作。
  Bagging算法是一种集成学习算法，全称为自助聚集算法（Bootstrap aggregating），顾名思义算法由 Bootstrap 与 Aggregating 两部分组成。（如下图展示了Bagging 算法使用自助取样（Bootstrapping4）生成多个子数据的示例）
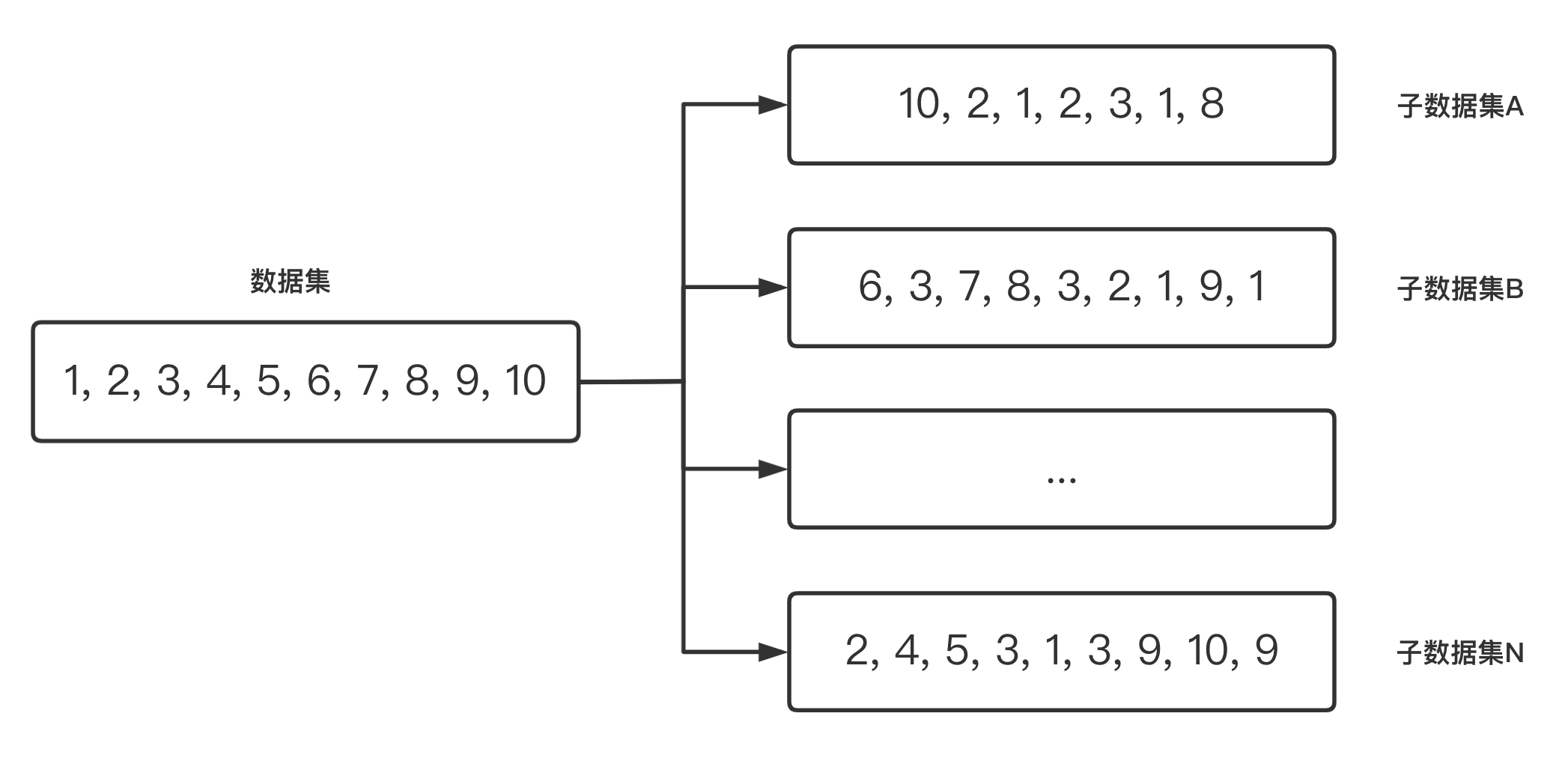算法的具体步骤为：假设有一个大小为 N 的训练数据集，每次从该数据集中有放回的取选出大小为 M 的子数据集，一共选 K 次，根据这 K 个子数据集，训练学习出 K 个模型。当要预测的时候，使用这 K 个模型进行预测，再通过取平均值或者多数分类的方式，得到{BANNED}最佳后的预测结果。

4.随机森林算法

（1）将多个决策树结合在一起，每次数据集是随机有放回的选出，同时随机选出部分特征作为输入，所以该算法被称为随机森林算法。可以看到随机森林算法是以决策树为估计器的Bagging算法。
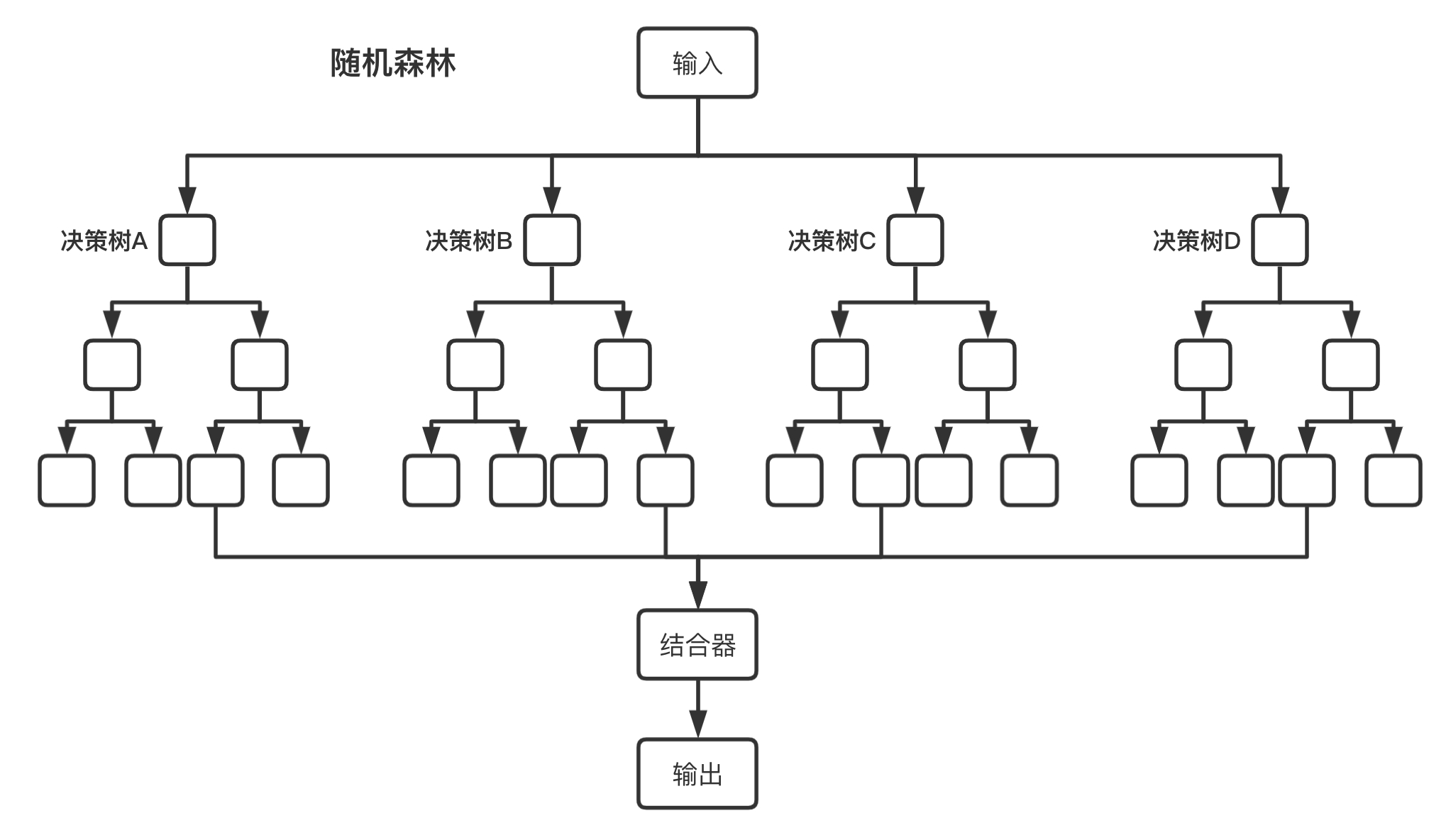    上图展示了随机森林算法的具体流程，其中结合器在分类问题中，选择多数分类结果作为{BANNED}最佳后的结果，在回归问题中，对多个回归结果取平均值作为{BANNED}最佳后的结果。
    使用Bagging算法能降低过拟合的情况，从而带来了更好的性能。单个决策树对训练集的噪声非常敏感，但通过Bagging算法降低了训练出的多颗决策树之间关联性，有效缓解了上述问题。

（2）随机森林算法步骤
            
             假设训练集 T 的大小为 N ，特征数目为 M ，随机森林的大小为 K ，随机森林算法的具体步骤如下：

遍历随机森林的大小 K 次：
??从训练集 T 中有放回抽样的方式，取样N 次形成一个新子训练集 D
??随机选择 m 个特征，其中 m < M
??使用新的训练集 D 和 m 个特征，学习出一个完整的决策树
得到随机森林

   上面算法中 m 的选择：对于分类问题，可以在每次划分时使用根号m个特征，对于回归问题， 选择M\3 ,但不少于 5 个特征。
(3)随机算法优缺点
 
随机森林算法的优点：
<1 对于很多种资料，可以产生高准确度的分类器
<2 可以处理大量的输入变量
<3 可以在决定类别时，评估变量的重要性
<4 在建造森林时，可以在内部对于一般化后的误差产生不偏差的估计
<5 包含一个好方法可以估计丢失的资料，并且如果有很大一部分的资料丢失，仍可以维持准确度
<6 对于不平衡的分类资料集来说，可以平衡误差
<7 可被延伸应用在未标记的资料上，这类资料通常是使用非监督式聚类，也可侦测偏离者和观看
<8 学习过程很快速
随机森林算法的缺点：
<1 牺牲了决策树的可解释性
<2 在某些噪音较大的分类或回归问题上会过拟合
<3 在多个分类变量的问题中，随机森林可能无法提高基学习器的准确性

5.代码实现

import numpy as np
from sklearn.tree import DecisionTreeClassifier


class rfc:
    """
    随机森林分类器
    """


    def __init__(self, n_estimators = 100, random_state = 0):
        # 随机森林的大小
        self.n_estimators = n_estimators
        # 随机森林的随机种子
        self.random_state = random_state


    def fit(self, X, y):
        """
        随机森林分类器拟合
        """
        self.y_classes = np.unique(y)
        # 决策树数组
        dts = []
        n = X.shape[0]
        rs = np.random.RandomState(self.random_state)
        for i in range(self.n_estimators):
            # 创建决策树分类器
            dt = DecisionTreeClassifier(random_state=rs.randint(np.iinfo(np.int32).max), max_features = "auto")
            # 根据随机生成的权重，拟合数据集
            dt.fit(X, y, sample_weight=np.bincount(rs.randint(0, n, n), minlength = n))
            dts.append(dt)
        self.trees = dts


    def predict(self, X):
        """
        随机森林分类器预测
        """
        # 预测结果数组
        probas = np.zeros((X.shape[0], len(self.y_classes)))
        for i in range(self.n_estimators):
            # 决策树分类器
            dt = self.trees[i]
            # 依次预测结果可能性
            probas += dt.predict_proba(X)
        # 预测结果可能性取平均
        probas /= self.n_estimators
        # 返回预测结果
        return self.y_classes.take(np.argmax(probas, axis = 1), axis = 0)

使用 Python 实现随机森林回归：

import numpy as np
from sklearn.tree import DecisionTreeRegressor


class rfr:
    """
    随机森林回归器
    """


    def __init__(self, n_estimators = 100, random_state = 0):
        # 随机森林的大小
        self.n_estimators = n_estimators
        # 随机森林的随机种子
        self.random_state = random_state


    def fit(self, X, y):
        """
        随机森林回归器拟合
        """
        # 决策树数组
        dts = []
        n = X.shape[0]
        rs = np.random.RandomState(self.random_state)
        for i in range(self.n_estimators):
            # 创建决策树回归器
            dt = DecisionTreeRegressor(random_state=rs.randint(np.iinfo(np.int32).max), max_features = "auto")
            # 根据随机生成的权重，拟合数据集
            dt.fit(X, y, sample_weight=np.bincount(rs.randint(0, n, n), minlength = n))
            dts.append(dt)
        self.trees = dts


    def predict(self, X):
        """
        随机森林回归器预测
        """
        # 预测结果
        ys = np.zeros(X.shape[0])
        for i in range(self.n_estimators):
            # 决策树回归器
            dt = self.trees[i]
            # 依次预测结果
            ys += dt.predict(X)
        # 预测结果取平均
        ys /= self.n_estimators
        return ys