AVL树

AVL树定义:
    AVL树是最早提出的自平衡二叉树，在AVL树中任何节点的两个子树的高度最大差别为一，所以它也被称为高度平衡树。
    AVL树得名于它的发明者G.M. Adelson-Velsky和E.M. Landis。AVL树种查找、插入和删除在平均和最坏情况下都是O（log n），
    增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。                                                                             
AVL树特点:
    1.本身首先是一棵二叉搜索树。
    2.带有平衡条件：每个结点的左右子树的高度之差的绝对值（平衡因子）最多为1
    也就是说，AVL树，本质上是带了平衡功能的二叉查找树（二叉排序树，二叉搜索树）。
AVL树的平衡因子（Balance Factor):
    等于该结点的左子树深度减去右子树深度的值称为平衡因子。平衡因子只可能是－1，0，1。
AVL树的最小不平衡子树：
    距离插入节点最近的，且平衡因子的绝对值大于1的节点为根的子树。
如下图，新插入节点37时，距离它最近的平衡因子绝对值超过1的节点是58，所以从58开始以下的子树为最小不平衡子树

平衡二叉树就是二叉树的构建过程中，每当插入一个结点，看是不是因为树的插入破坏了树的平衡性，若是，则找出最小不平衡树。在保持二叉树特性的前提下，调整最小不平衡子树中各个结点之间的链接关系，进行相应的旋转，使之成为新的平衡子树。简记为:步步调整，步步平衡。

当插入数据或者删除数据的时候，可能破坏树的平衡性。为了保持树的平衡性，需要对树进行旋转操作:
左旋转动画:

右旋转动画:

有四种种情况可能导致二叉查找树不平衡，分别为：

（1）LL：插入一个新节点到根节点的左子树（Left）的左子树（Left），导致根节点的平衡因子由1变为2

（2）RR：插入一个新节点到根节点的右子树（Right）的右子树（Right），导致根节点的平衡因子由-1变为-2

（3）LR：插入一个新节点到根节点的左子树（Left）的右子树（Right），导致根节点的平衡因子由1变为2

（4）RL：插入一个新节点到根节点的右子树（Right）的左子树（Left），导致根节点的平衡因子由-1变为-2

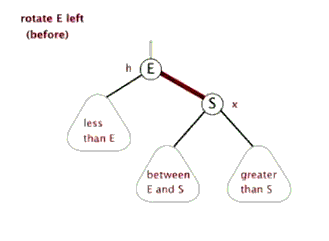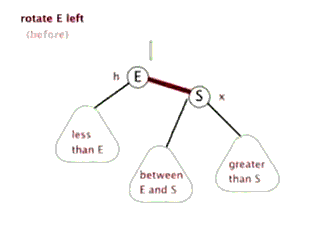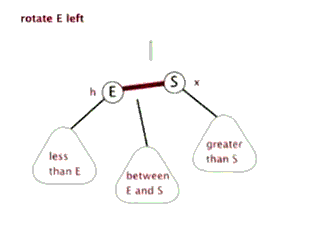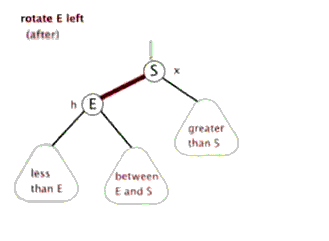
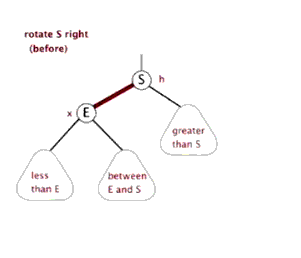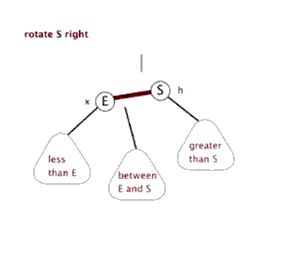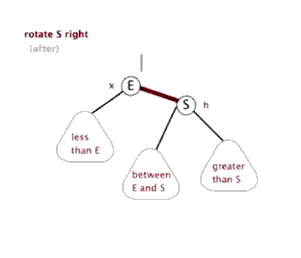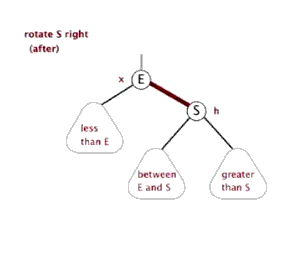
针对四种种情况可能导致的不平衡，可以通过旋转使之变平衡。有两种基本的旋转：

（1）左旋转：将根节点旋转到（根节点的）右孩子的左孩子位置

（2）右旋转：将根节点旋转到（根节点的）左孩子的右孩子位置

除了左旋和右旋，还有先左旋后右旋，先右旋后左旋。所有旋转如下图:


要理解旋转操作，有三个问题需要解决:
1)需要旋转的部分是什么
2)以什么为轴旋转,以及旋转结点是谁
3)什么时候该用什么旋转方式(左旋,右旋,左右旋,右左旋)

1)对于第一个问题:
    需要通过最小不平衡树来确定,通过最小不平衡树来确定需要旋转的部分是那些.
2)对于第二个问题:
    需要通过平衡因子来确定,平衡因子是±2结点与±1结点(插入或者删除结点到±2结点路径上)正负相同,则旋转轴为±1结点,旋转结点是±2结点.如果正负号不同,则旋转轴为±1结点子结点(插入或者删除结点到±2结点路径上),旋转结点为±1结点.
3)对于第三个问题:
    需要根据平衡因子的状态来确定,如果旋转轴结点和旋转结点平衡因子符号相同,旋结点为负号则使用左旋,如果正号则使用右旋.如果旋转轴结点和旋转结点平衡因子符号不同，旋转结点是正,则使用右左旋转,否则使用左右旋转.

通过上述三个问题就可以分析下面的图:(右旋是顺时针旋转,左旋是逆时针旋转)

1. 新建AVL树
   新建AVL树的根节点root。 

2. 依次添加"3,2,1,4,5,6,7,16,15,14,13,12,11,10,8,9" 到AVL树中，过程如下。
2.01 添加3,2
添加3,2都不会破坏AVL树的平衡性。

2.02 添加1
添加1之后，AVL树失去平衡，此时需要对AVL树进行旋转(右旋)。旋转过程如下：

2.03 添加4
添加4不会破坏AVL树的平衡性。

2.04 添加5
添加5之后，AVL树失去平衡，此时需要对AVL树进行旋转(左旋转)。旋转过程如下：

2.05 添加6
添加6之后，AVL树失去平衡，此时需要对AVL树进行旋转(左旋转)。旋转过程如下：

2.06 添加7
添加7之后，AVL树失去平衡，此时需要对AVL树进行旋转(左旋转)。旋转过程如下：

2.07 添加16
添加16不会破坏AVL树的平衡性。

2.08 添加15
添加15之后，AVL树失去平衡，此时需要对AVL树进行旋转(右左旋转)。旋转过程如下：

2.09 添加14
添加14之后，AVL树失去平衡，此时需要对AVL树进行旋转(右左旋转)。旋转过程如下：

2.10 添加13
添加13之后，AVL树失去平衡，此时需要对AVL树进行旋转(左旋转)。旋转过程如下：

2.11 添加12
添加12之后，AVL树失去平衡，此时需要对AVL树进行旋转(右旋转)。旋转过程如下：

2.12 添加11
添加11之后，AVL树失去平衡，此时需要对AVL树进行旋转(右旋转)。旋转过程如下：

2.13 添加10
添加10之后，AVL树失去平衡，此时需要对AVL树进行旋转(右旋转)。旋转过程如下：

2.14 添加8
添加8不会破坏AVL树的平衡性。

2.15 添加9
但是添加9之后，AVL树失去平衡，此时需要对AVL树进行旋转(左右旋转)。旋转过程如下：

3. 打印树的信息
输出下面树的信息：

参考链接:


http://www.cnblogs.com/skywang12345/p/3576969.html

http://blog.csdn.net/collonn/article/details/20128205