二叉树三种周游（traversal）方式

遍历序列

1．遍历二叉树的执行踪迹
    　三种递归遍历算法的搜索路线相同（如下图虚线所示）。 
具体线路为：
    　从根结点出发，逆时针沿着二叉树外缘移动，对每个结点均途径三次，最后回到根结点。
        

2．遍历序列

（1） 中序序列
    中序遍历二叉树时，对结点的访问次序为中序序列
　【例】中序遍历上图所示的二叉树时，得到的中序序列为：
                D B A E C F
（2） 先序序列
    先序遍历二叉树时，对结点的访问次序为先序序列
    【例】先序遍历上图所示的二叉树时，得到的先序序列为：
                A B D C E F
（3） 后序序列
    　后序遍历二叉树时，对结点的访问次序为后序序列
　【例】后序遍历上图所示的二叉树时，得到的后序序列为：
                D B E F C A
  注意：
　　（1） 在搜索路线中，若访问结点均是第一次经过结点时进行的，则是前序遍历；若访问结点均是在第二次(或第三次)经过结点时进行的，则是中序遍历(或后序遍历)。只要将搜索路线上所有在第一次、第二次和第三次经过的结点分别列表，即可分别得到该二叉树的前序序列、中序序列和后序序列。
　　（2） 上述三种序列都是线性序列，有且仅有一个开始结点和一个终端结点，其余结点都有且仅有一个前趋结点和一个后继结点。为了区别于树形结构中前趋(即双亲)结点和后继(即孩子)结点的概念，对上述三种线性序列，要在某结点的前趋和后继之前冠以其遍历次序名称。
【例】上图所示的二叉树中结点C，其前序前趋结点是D，前序后继结点是E；中序前趋结点是E，中序后继结点是F；后序前趋结点是F，后序后继结点是A。但是就该树的逻辑结构而言，C的前趋结点是A，后继结点是E和F。

遍历算法

1．中序遍历的递归算法定义：
    　若二叉树非空，则依次执行如下操作：
         (1)遍历左子树；
         (2)访问根结点；
         (3)遍历右子树。

2．先序遍历的递归算法定义：
   　若二叉树非空，则依次执行如下操作：
         (1) 访问根结点；
         (2) 遍历左子树；
         (3) 遍历右子树。

3．后序遍历得递归算法定义：
   　若二叉树非空，则依次执行如下操作：
         (1)遍历左子树；
         (2)遍历右子树；
         (3)访问根结点。

preorder(bintree t)
　{//对二叉树进行先序遍历
　　if (t){
　　　printf("%c",t->data);
　　　preorder(t->lchild);
　　　preorder(t->rchild);
　　}//end of if
　}//end of preorder
　 
inorder(bintree t)
　{//对二叉树进行中序遍历
　　if (t){
　　　　　　　inorder(t->lchild);
　　　　　　　printf("%c",t->data);
　　　　　　　inorder(t->rchild);
　　　　　}//end of if
　}//end of inorder

postorder(bintree t)
　{//对二叉树进行后序遍历
　　if (t){
　　　　　　postorder(t->lchild);
　　　　　　postorder(t->rchild);
　　　　　　printf("%c",t->data);
　　　　　}//end of if
　}//end of postorder

二叉链表的构造

1． 基本思想
    　基于先序遍历的构造，即以二叉树的先序序列为输入构造。
  注意：
    　先序序列中必须加入虚结点以示空指针的位置。
　【例】
　　建立上图所示二叉树，其输入的先序序列是：ABD∮∮CE∮∮F∮∮。

2． 构造算法
    　假设虚结点输入时以空格字符表示，相应的构造算法为：
    　void CreateBinTree (BinTree *T)
      { //构造二叉链表。T是指向根指针的指针，故修改*T就修改了实参(根指针)本身
        char ch；
        if((ch=getchar())=='') *T=NULL； //读人空格，将相应指针置空 
        else{ //读人非空格
              *T=(BinTNode *)malloc(sizeof(BinTNode))； //生成结点
              (*T)->data=ch；
              CreateBinTree(&(*T)->lchild)； //构造左子树
              CreateBinTree(&(*T)->rchild)； //构造右子树
             }
      }
  注意：
    　调用该算法时，应将待建立的二叉链表的根指针的地址作为实参。
【例】
　设root是一根指针(即它的类型是BinTree)，则调用CreateBinTree(&root)后root就指向了已构造好的二叉链表的根结点。

 附源代码

#include
#include
typedef char datatype;
typedef struct node
{
    datatype data;
    struct node *lchild,*rchild;
}bintnode;
typedef bintnode *bintree;

    void createbintree(bintree *t)
    {
    //输入二叉树的先序遍历序列，创建二叉链表
        char ch;
        ch=getchar();
        if(ch=='#')
            *t=NULL;//如果读入空格字符，创建空树，T是指向指针的指针,*t就相当于一个bintree指针，专门指向bintnode；
        else
        {
            (*t)=(bintnode*)malloc(sizeof(bintnode));
            (*t)->data=ch;
            createbintree(&(*t)->lchild);//根据先序遍历，继续创建左子树，让客户端继续输入
            createbintree(&(*t)->rchild);//创建完左子树，继续创建右子树
        } //递归调用，自动返回
    }
    void preorder(bintree t)
    {
        if(t)
        {
            printf("%c ",t->data);//先访问根结点，再遍历左子树，跟着右子树
            preorder(t->lchild);
            preorder(t->rchild);
        }

    }
    void inorder(bintree t)
    {
        if(t)
        {
            inorder(t->lchild);
            printf("%c ",t->data);//
            inorder(t->rchild);
        }
    }
    void postorder(bintree t)
    {
        if(t)
        {
            postorder(t->lchild);
            postorder(t->rchild);
            printf("%c ",t->data);//
        }
    }
int main()
{

/*
这里的输入要严格按照正确的顺序才能结束.这里要用到二叉树的一个性质,
就是说对于有n个节点的二叉树,就有n+1个空域,在这里即为如果你输入了n个
元素,那么一定要有n+1个#才会结束迭代过程.
*/
    bintree t=NULL;
    createbintree(&t);//这样才能改变T，指向指针的指针
    preorder(t);
    printf("\n");
    inorder(t);
    printf("\n");
    postorder(t);
    printf("\n");
    getchar();
    return 0;
}
/*
输入:ABDH##I##EJ##K##CF#L##G##
前序遍历:A B D H I E J K C F L G
中序遍历:H D I B J E K A F L C G
后序遍历:H I D J K E B L F G C A
*/

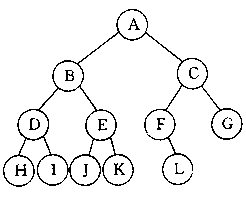
输入:ABDH##I##EJ##K##CF#L##G##
前序遍历:A B D H I E J K C F L G
中序遍历:H D I B J E K A F L C G
后序遍历:H I D J K E B L F G C A