惊人的答案：平均要取多少个(0,1)中的随机数才能让和超过1

数学常数最令人着迷的就是，它们常常出现在一些看似与之毫不相干的场合中。 随便取一个 0 到 1 之间的数，再加上另一个 0 到 1 之间的随机数，然后再加上一个 0 到 1 之间的随机数……直到和超过 1 为止。一个有趣的问题：平均需要加多少次，才能让和超过 1 呢？答案是 e 次。

  

 
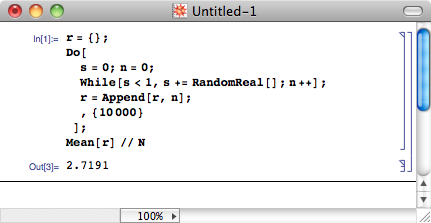
    为了证明这一点，让我们先来看一个更简单的问题：任取两个 0 到 1 之间的实数，它们的和小于 1 的概率有多大？容易想到，满足 x+y<1 的点 (x, y) 占据了正方形 (0, 1)×(0, 1) 的一半面积，因此这两个实数之和小于 1 的概率就是 1/2 。类似地，三个数之和小于 1 的概率则是 1/6 ，它是平面 x+y+z=1 在单位立方体中截得的一个三棱锥。这个 1/6 可以利用截面与底面的相似比关系，通过简单的积分求得：

       ∫(0..1) (x^2)*1/2 dx = 1/6

  

 
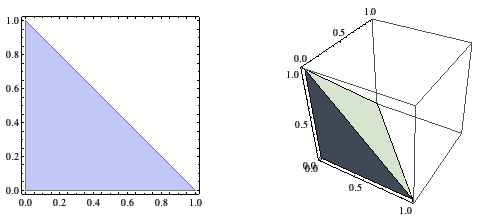
    可以想到，四个 0 到 1 之间的随机数之和小于 1 的概率就等于四维立方体一角的“体积”，它的“底面”是一个体积为 1/6 的三维体，在第四维上对其进行积分便可得到其“体积”

       ∫(0..1) (x^3)*1/6 dx = 1/24

    依此类推， n 个随机数之和不超过 1 的概率就是 1/n! ，反过来 n 个数之和大于 1 的概率就是 1 - 1/n! ，因此加到第 n 个数才刚好超过 1 的概率就是

       (1 - 1/n!) - (1 - 1/(n-1)!) = (n-1)/n!

    因此，要想让和超过 1 ，需要累加的期望次数为

       ∑(n=2..∞) n * (n-1)/n! = ∑(n=1..∞) n/n! = e

---http://www.matrix67.com/blog/archives/3507