Buddy System 内存管理

Buddy System是一种经典的内存管理算法. 在Unix和Linux操作系统中都有用到. 其作用是减少存储空间中的空洞, 减少碎片, 增加利用率.

在Webus空间管理组件(WSM)中, 我也提供了Buddy System的实现, 关于这种算法的详细描述, 建议大家看经典教材 " 数据结构" 一书第8章第4节.
 呵呵, 蓝色经典!

我在此仅谈谈如下三个问题:
1. Buddy System的基本原理?
2. 如何分配空间?
3. 如何回收空间?

对以上三个问题的说明:
Buddy System把系统中的可用存储空间划分为存储块(Block)来进行管理, 每个存储块的大小必须是2的n次幂(Pow(2, n)), 即1, 2, 4, 8, 16, 32, 64, 128...
假设系统全部可用空间为Pow(2, k), 那么在Buddy System初始化时将生成一个长度为k + 1的可用空间表List, 并将全部可用空间作为一个大小为Pow(2, k)的块挂接在List的最后一个节点上, 如下图:

当用户申请size个字的存储空间时, Buddy System分配的Block大小为Pow(2, m)个字大小(Pow(2, m-1) < size < Pow(2,  m)).
此时Buddy System将在List中的m位置寻找可用的Block. 显然List中这个位置为空, 于是Buddy System就开始寻找向上查找m+1, m+2, 直到达到k为止. 找到k后, 便得到可用Block(k), 此时Block(k)将分裂成两个大小为Pow(k-1)的块, 并将其中一个插入到List中k-1的位置, 同时对另外一个继续进行分裂. 如此以往直到得到两个大小为Pow(2, m)的块为止, 如下图所示:
 
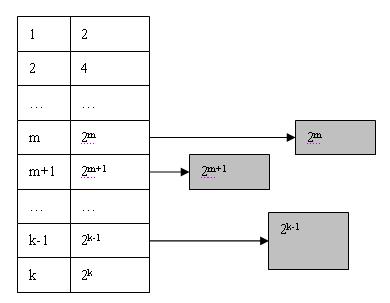
如果系统在运行一段时间之后, List中某个位置n可能会出现多个块, 则将其他块依次链接可用块链表的末尾:

当Buddy System要在n位置取可用块时, 直接从链表头取一个就行了.

当一个存储块不再使用时, 用户应该将该块归还给Buddy System. 此时系统将根据Block的大小计算出其在List中的位置, 然后插入到可用块链表的末尾. 在这一步完成后, 系统立即开始合并操作. 该操作是将"伙伴"合并到一起, 并放到List的下一个位置中, 并继续对更大的块进行合并, 直到无法合并为止.

何谓"伙伴"? 如前所述, 在分配存储块时经常会将一个大的存储块分裂成两个大小相等的小块, 那么这两个小块就称为"伙伴".在Buddy System进行合并时, 只会将互为伙伴的两个存储块合并成大块, 也就是说如果有两个存储块大小相同, 地址也相邻, 但是不是由同一个大块分裂出来的, 也不会被合并起来. 正常情况下, 起始地址为p, 大小为Pow(2, k)的存储块, 其伙伴块的起始地址为: p + Pow(2, k) 和 p - Pow(2, k).

下面把数据结构一书中Buddy算法分配存储块的C++伪码帖出来以供大家参考:

Space AllocBuddy(FreeList &avail, int n)
{
    //avail[0..m]为可利用空间表, n为申请分配量, 若有不小于n的空闲块,
    //则分配相应的存储块, 并返回其首地址, 否则返回NULL
    for(k=0; k<=m && (avail[k].nodesize < n+1 || !avail[k].first); ++k);//查找满足分配要求的子表
    if(k>m) return NULL;//分配失败, 返回NULL;
    else {//可进行分配
        pa = avail[k].first;//指向可分配子表的第一个节点
        pre = pa->llink; suc = pa->rlink;//分配指向前驱和后继
        if(pa == suc) avail[k].first = NULL;//分配后该子表变为空表
        else {//从子表删除*pa节点
            pre->rlink = suc; suc->llink = pre; avail[k].first = suc;
        }
    }
    for(i = 1; avail[k-i].nodesize >= n+1; ++i) {
        pi = pa + pow(2, k-i); pi-> rlink = pi; pi ->llink = pi;
        pi -> tag = 0; pi -> kval = k-i; avail[k-i].first = pi;
    }//将剩余块插入相应子表
    pa -> tag = 1; pa -> kval = k-(--i);
    return pa;
}

基于哈希查找的基本思想与结构定义

3.1 基于哈希查找的基本思想

    基于哈希查找的基本思想是：利用哈希快速查找优点和空闲块在可利用空间表中的分布规律，构造哈希函数。当请求分配存储空间时，通过查找以空闲块大小为关键字的哈希表选择合适的空闲块链，实现最佳分配策略。

    对系统运行可能形成的k个空闲块链表，将头指针组织成一个向量结构，根据链表中空闲块大小确定链表头指针在向量中的位置。

    由于申请的空闲块长度 n 要求满足关系2^i－1 < n ≤2ⁱ。因此可定义哈希函数如下：

   

    哈希函数计算结果确定了所申请大小的空闲块对应链表应在向量表中的位置。

3.2 存储结构定义

    空闲块结点结构定义，如图1所示。

 图1 空闲块结点结构

    结点数据类型定义描述如下：

    #define n size /*定义size为可利用空间容量，大小为2的次幂*/

    typedef struct WORD_NODE                               

    { int  tag; /*块标志，0：空闲，1：占用*/

       int  kval; /*块大小，值为2的K次幂*/

        WORD_NODE  *llink,rlink; /*指向前驱、后继结点的指针域*/

        OtherType  other;  /*其它部分*/

    }WORD_NODE,head;     /*内存字类型，结点的第一个字为head*/

    头指针向量表数据类型定义描述如下：

    typedef struct HeadNode

   { int nodesize;  /*该链表空闲块大小*/

   WORD_NODE  *first; /*该链表的头指针 */

  }FreeList[m+1]；/*可利用空间表头向量类型*/

    系统初始状态的可利用空间表状如图2所示。

 图2 可利用空间表初始状态

 

 

4  分配与回收算法

4．1 分配算法

    当用户申请分配长度为n 的存储块时, 求 i = HASH(n),若FreeList[i].first不空，只要删除此链表中的第一个结点，分配给申请者即可；否则判断FreeList[i＋1]所对应的空闲块链表，若不空，则把长为2^i＋1 的第一个空闲块分为等长的两半(一对伙伴) , 一个用于分配给申请者，另一个链入FreeList[i].first对应的链表中。若FreeList[i＋1].first仍然为空，则依次判 FreeList[i＋2].first，以此类推。假若直到i＋k 时，FreeList[i＋k].first非空，则需要从该链表中取出一个结点，将大小为2^k的一部分分配给申请者，剩余部分分割成若干个大小分别为²ⁱ⁺¹、2ⁱ⁺²、…、2^i+k-1的结点插入到对应大小的链表中。

     算法描述如下：

      WORD_NODE *AllocBuddy(FreeList &avail,int n)

    {/*申请容量为n的存储空间*/

        j = HASH(n);

       while(!avail[j].first&&j<=m) j++;

        if(j > m)return NULL;

           i = j;

          pa = avail[i].first;

          pre = pa->llink;suc = pa->rlink;

      if(pa == suc) avail[i].first = NULL;

       else {从子表删去*pa结点;}

         for(k = j;k < i;k++)

         { pi = pa + 2i-k;

           pi->rlink = pi;

           pi->llink = pi;

           pi->tag = 0;

          pi->kval = i-k;

      avail[i-k].first = pi

          }

          Pa->tag = 1;

          pa->kval = i-(--k);

         Return pa;

      }

4．2 回收算法

    回收空闲块时，若该回收块的伙伴也为空闲块，则需将他们合并成大的空闲块。然后再判断合并后的空闲块的伙伴是否为空闲块，若是则继续合并。否则只要将释放的空闲块简单地插入到相应空闲块链表中即可。

    设大小为2ⁱ的空闲块起始地址为 p，其伙伴块的起始地址可采用下式计算:

    若p MOD 2ⁱ⁺¹ =0，则其伙伴块的起始地址为p+2ⁱ

    若p MOD 2ⁱ⁺¹ =2ⁱ，则其伙伴块的起始地址为p-2ⁱ

    例如，假设p为大小为2ⁱ的空闲块的起始地址，当p MOD 2ⁱ⁺¹ =0时，起始地址为p和p＋2ⁱ的两个空闲块互为伙伴；当p MOD 2ⁱ⁺¹ =2ⁱ时，起始地址为p和p－2ⁱ的两个空闲块互为伙伴。利用该性质可方便地实现空闲块的合并与回收。这里仅给出回收算法的描述如下：

void FreeBuddy(&avail,*addr,n)

{  /*回收长度为n，起始地址为addr的块*/

置回收块标志tag为0，块长kval为n;

求回收块的伙伴地址buddy=addr%(2* n)?(addr- n):addr+n);

求回收块应在头指针向量中的位置i=HASH（n）;

如果avail[i].first为空，表明该块没有伙伴，直接插入到插入到该链表中;

否则{

在当前链表中寻找伙伴（地址为buddy的块）;

如果存在伙伴，并且该伙伴是当前链表中唯一大小为2i的空闲块,则置avail[i].first为空;

否则，从当前链表中删去伙伴;

修改合并后的新空闲块起始地址（addr或buddy）以及合并块kval的值为2*n;

以新地址和新块长为参数，递归调用FreeBuddy函数，继续调用并合并伙伴块;

}

  将得到的最后合并块插入到对应头指针向量所对应的空闲块链表中;

}

5  结束语

    操作系统动态内存管理方法很多，它们各有其优缺点，各有其适用情形。选择合理的存储分配和管理方案必须建立在设计者对硬件平台和系统中动态内存的申请释放流进行科学评价和分析的基础上。

    本文所提出的存储管理算法的时间性能主要取决于查找空闲块的位置和分割、合并空闲块所花费的时间。采用哈希快速定位方法查找空闲块的时间为常量，合并空闲块的时间开销为k的线性阶，分配、释放空闲空间的时耗极小且相对稳定，比较适用于嵌入式实时系统。但由于释放存储空间时只归并互为伙伴的空闲块，容易产生存储碎片。
--------

基于Buddy动态存储管理算法的应用研究

李庆亮^1,2，张新成^1,2，戚新波<sup>1,2

http://www.cnblogs.com/iamzyf</sup>