参考文献:
对于ax+b这种情形,线性回归函数,例如最小二乘法是可以解决这些问题的,但是对于多维变量函数f(x,y)而言,就无法很好的解决了。

为了能够得到多维变量的回归函数,h(x)表示的是房屋的价格,根据输入的变量所产生的输出,我们采用如下方式组织各个影响因素。
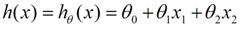
但是各个xn前面的参数是无法确定的,因此可以采用梯度下降的方法来确定Θn的值。
根据最小二乘法,得到误差函数J(Θ),目标是计算出各个θ,使得J(θ)最小。

下面就是计算梯度下降的方法:
1. 随机初始化θ
2. 迭代,如果新的θ能够获得使得J(θ)更小
3. 如果J(θ)能够继续减小,那么回到2,继续执行

下面介绍偏导J(θ)的方法:

根据样本值y和拟合函数hθ(x),以及xj,获得理想的拟合函数hθ(x).
当用户有m组数据的时候,求解各个θ的值。
方法如下;

阅读(20460) | 评论(0) | 转发(0) |