更复杂些的滤波算子一般是先利用高斯滤波来平滑,然后计算其1阶和2阶微分。由于它们滤除高频和低频,因此称为带通滤波器(band-pass filters)。
在介绍具体的带通滤波器前,先介绍必备的图像微分知识。
1 一阶导数
连续函数,其微分可表达为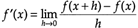 ,或
,或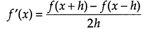 (1.1)
(1.1)
对于离散情况(图像),其导数必须用差分方差来近似,有
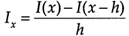 ,前向差分 forward differencing (1.2)
,前向差分 forward differencing (1.2)
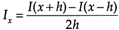 ,中心差分 central differencing (1.3)
,中心差分 central differencing (1.3)
1)前向差分的Matlab实现
| 01 | function dimg = mipforwarddiff(img,direction) |
| 02 | % MIPFORWARDDIFF Finite difference calculations |
| 04 | % DIMG = MIPFORWARDDIFF(IMG,DIRECTION) |
| 06 | % Calculates the forward-difference for a given direction |
| 08 | % DIRECTION : 'dx' or 'dy' |
| 09 | % DIMG : resultant image |
| 11 | % See also MIPCENTRALDIFF MIPBACKWARDDIFF MIPSECONDDERIV |
| 12 | % MIPSECONDPARTIALDERIV |
| 14 | % Omer Demirkaya, Musa Asyali, Prasana Shaoo, ... 9/1/06 |
| 15 | % Medical Image Processing Toolbox |
| 17 | imgPad = padarray(img,[1 1],'symmetric','both');%将原图像的边界扩展 |
| 18 | [row,col] = size(imgPad); |
| 22 | dimg(:,1:col-1) = imgPad(:,2:col)-imgPad(:,1:col-1);%x方向差分计算, |
| 24 | dimg(1:row-1,:) = imgPad(2:row,:)-imgPad(1:row-1,:); |
| 25 | otherwise, disp('Direction is unknown'); |
| 27 | dimg = dimg(2:end-1,2:end-1); |
2)中心差分的Matlab实现
| 01 | function dimg = mipcentraldiff(img,direction) |
| 02 | % MIPCENTRALDIFF Finite difference calculations |
| 04 | % DIMG = MIPCENTRALDIFF(IMG,DIRECTION) |
| 06 | % Calculates the central-difference for a given direction |
| 08 | % DIRECTION : 'dx' or 'dy' |
| 09 | % DIMG : resultant image |
| 11 | % See also MIPFORWARDDIFF MIPBACKWARDDIFF MIPSECONDDERIV |
| 12 | % MIPSECONDPARTIALDERIV |
| 14 | % Omer Demirkaya, Musa Asyali, Prasana Shaoo, ... 9/1/06 |
| 15 | % Medical Image Processing Toolbox |
| 17 | img = padarray(img,[1 1],'symmetric','both'); |
| 22 | dimg(:,2:col-1) = (img(:,3:col)-img(:,1:col-2))/2; |
| 24 | dimg(2:row-1,:) = (img(3:row,:)-img(1:row-2,:))/2; |
| 26 | disp('Direction is unknown'); |
| 28 | dimg = dimg(2:end-1,2:end-1); |
实例:技术图像x方向导数
| 1 | I = imread('coins.png'); figure; imshow(I); |
| 2 | Id = mipforwarddiff(I,'dx'); figure, imshow(Id); |


原图像 x方向1阶导数
2 图像梯度(Image Gradient)
图像I的梯度定义为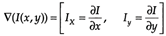 ,其幅值为
,其幅值为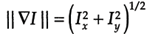 。出于计算性能考虑,幅值也可用
。出于计算性能考虑,幅值也可用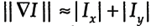 来近似。
来近似。
Matlab函数
1)gradient:梯度计算
2)quiver:以箭头形状绘制梯度。注意放大下面最右侧图可看到箭头,由于这里计算横竖两个方向的梯度,因此箭头方向都是水平或垂直的。
实例:仍采用上面的原始图像
| 1 | I = double(imread('coins.png')); |
| 3 | magnitudeI=sqrt(dx.^2+dy.^2); |
| 4 | figure;imagesc(magnitudeI);colormap(gray);%梯度幅值 |
| 5 | hold on;quiver(dx,dy);%叠加梯度方向 |

梯度幅值 梯度幅值+梯度方向
3 二阶导数
对于一维函数,其二阶导数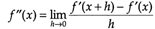 ,即
,即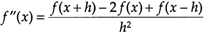 。它的差分函数为
。它的差分函数为
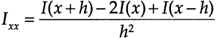 (3.1)
(3.1)
3.1 普拉斯算子(laplacian operator)
3.1.2 概念
拉普拉斯算子是n维欧式空间的一个二阶微分算子。它定义为两个梯度向量算子的内积
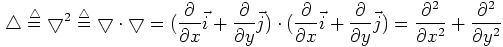 (3.2)
(3.2)
其在二维空间上的公式为: 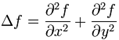 (3.3)
(3.3)
对于1维离散情况,其二阶导数变为二阶差分
1)首先,其一阶差分为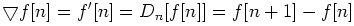
2)因此,二阶差分为
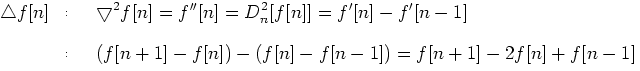
3)因此,1维拉普拉斯运算可以通过1维卷积核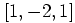 实现
实现
对于2维离散情况(图像),拉普拉斯算子是2个维上二阶差分的和(见式3.3),其公式为:
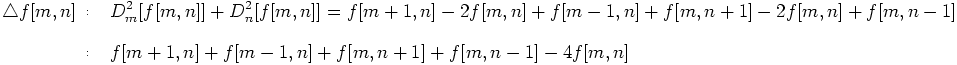 (3.4)
(3.4)
上式对应的卷积核为
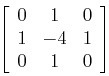
常用的拉普拉斯核有:
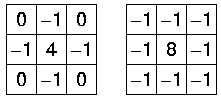
3.1.2 应用
拉普拉斯算子会突出像素值快速变化的区域,因此常用于边缘检测。
Matlab里有两个函数
1)del2
计算公式: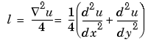 ,
,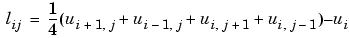
2)fspecial:图像处理中一般利用Matlab函数fspecial
h = fspecial('laplacian', alpha) returns a 3-by-3 filter approximating the shape of the two-dimensional Laplacian operator.
The parameter alpha controls the shape of the Laplacian and must be in the range 0.0 to 1.0. The default value for alpha is 0.2.
3.1.3 资源
(非常清晰的Laplacian Operator介绍,本文的主要参考)
![]() ,前向差分 forward differencing (1.2)
,前向差分 forward differencing (1.2)![]() ,中心差分 central differencing (1.3)
,中心差分 central differencing (1.3)![]() ,其幅值为
,其幅值为![]() 。出于计算性能考虑,幅值也可用
。出于计算性能考虑,幅值也可用![]() 来近似。
来近似。![]() (3.3)
(3.3)