分类:
2010-02-01 01:01:50
1.3 计算机图形学数学基础和图形变换
提到D3D中应用广泛的图形变换之前,不得不说一下与图形学有关的数学基础,这里只温习点、向量和矩阵。
此节包含:
1.3.1 坐标参照系
1.3.2 点和向量
1.3.2.1 向量相加与定比例相乘
1.3.2.2 两个向量的标量积 (点积、点乘)
1.3.2.3 两向量的向量积 (叉积)
1.3.2.4 点、向量与D3D
1.3.3 矩阵
1.3.3.1 标量乘法和矩阵加法
1.3.3.2 矩阵乘法
1.3.3.3 矩阵转置
1.3.3.4 矩阵的秩
1.3.3.5 矩阵的逆矩阵
1.3.3.6 矩阵与D3D
1.3.4 复数和四元数
1.3.5 图形变换
1.3.5.1 齐次坐标
1.3.5.2 二维图形几何变换
1.3.5.3 三维图形几何变换
1.3.5.3.1 基本变换
1.3.5.3.2 特殊变换
1.3.5.3.3 投影变换
////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
1.3.1 坐标参照系
为了更好的在图形设备上来显示内容,通常需要一个标准来定位,某种角度来说好似经纬度的作用一般。
二维笛卡尔坐标参照系中,系统原点大多处于屏幕左上角(也有屏幕中央的)。当然了,为了适合各种项目的需要,可能也会从新定义坐标参照系。
还有一些坐标系,比如Polar Coordinates(极坐标系)、柱面坐标系球面坐标系等,这些的相关内容就先略过了。笛卡尔坐标系和极坐标系的变换,可以由三角函数得到:
_______
r=√x2+y2 θ =tan-1(y/x) θ(radian)=s/r (s为弧长)
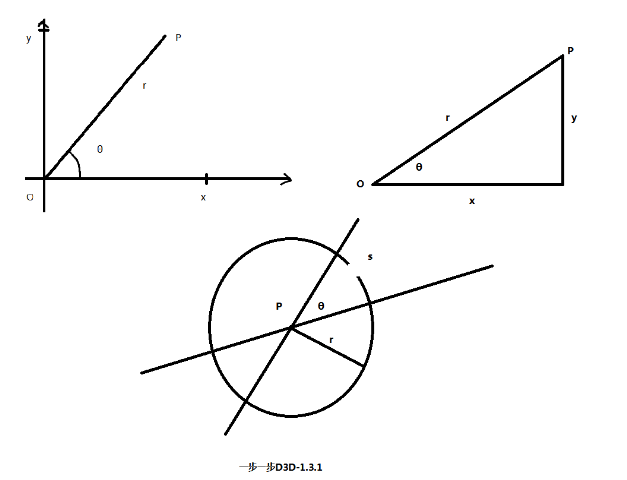
此外还有三维笛卡尔坐标系,这里就需要注意使用的时候是左手坐标系还是右手坐标系。比较常用的就是笛卡尔直角坐标系了,也叫正交坐标系。
1.3.2 点和向量
点和向量的概念有根本的区别。点是某参照系以坐标值指定的位置,一个向量(矢量)定义为两个点位置之间的差。它有大小,有方向。对于二维向量来说:
V=P2-P1
=(x2-x1,y2-y1)
=(Vx,Vy)
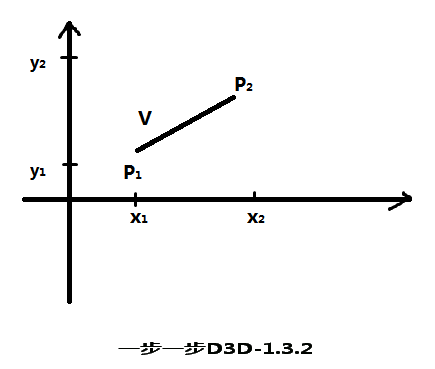
Vx,Vy分别是V在X轴和Y轴上的投影,给定两点位置可得任何坐标系下的向量分量。
所以二维向量V的大小便是:
___________ ________________
|V|=√ Vx2+Vy2 =√(x2-x1)2+(y2-y1)2
它的方向可以根据离x轴的角位移量给出:
α=tan-1(Vy/Vx)
而如果是三维空间向量大小则为:
_______________
|V|=√ Vx2+Vy2+Vz2
V,即是向量的长度也叫做向量的模。
此中向量的方向由方向角α、β、γ给出,其实就是求该向量与各个坐标轴形成的角:
cosα=Vx / |V|` cosβ=Vy / |V|` cosγ=Vz / |V|
cosα、cosβ、cosγ为向量的方向余弦。实际上为指定V的方向,只需两个方向余弦。因为:
cos2α+cos2β+cos2γ=1
1.3.2.1 向量相加与定比例相乘
V1+V2=(V1x+V2x, V1y+V2y, V1z+V2z)
向量与标量相加无意义。因为标量是一个数值,向量可能有多个数值分量。
向量与标量的乘法(数乘):aV=(aVx,aVy,aVz)
1.3.2.2 两个向量的标量积
产生标量的向量乘法:V1*V2=|V1||V2|cosθ 0≤θ≤π
在笛卡尔坐标系中标量积(点乘)的计算: V1*V2= V1x*V2x + V1y*V2y + V1z*V2z
而点积是可以交换的:V1*V2 = V2*V1
点积(点乘)的关于向量是遵循加法分配律的:V1*(V2+V3)=V1*V2 + V1*V3
由标量积,我们可知:
两向量相乘:
结果等于0,则两向量互相垂直;
结果大于0,则两向量之间的夹角小于90度;
结果小于0,则两向量之间的夹角大于90度。
1.3.2.3 两向量的向量积 (叉积)
能产生一个向量的两个向量的乘法:V1 ×(注:叉乘) V2=u|V1||V2|sinθ 0≤θ≤π
u是垂直与V1 、 V2 的单位向量(1),而u的方向则取决于使用的坐标系是左手还是右手,拇指方向即为u的方向。这个积叫做两个向量的叉积(向量积)。它是垂直与两个向量所在平面的向量,他的大小等于这两个向量与坐标轴形成的平行四边形的面积。
当然,也可以借助指定坐标系的向量分量来表达叉积。笛卡尔坐标系中:
叉积的分量=V1 ×(叉乘) V2=(V1y*V2x - V1z*V2y , V1z*V2x - V1x*V2z , V1x*V2y - V1y*V2x)
如果令ux、uy、uz 表示沿x, y ,z 轴的单位向量, 那借助笛卡尔分量以行列格式写出叉积,则:
ux uy uz
V1 X V2 =| V1x V1y V1z |
V2x V2y V2z
任意两个平行向量的叉积是0。这里需要注意叉积并不满足交换律,而是满足反交换律 :V1 X V2 = -(V2 X V1)
此外,叉积并不满足结合律 V1 X (V2 X V3)≠(V1 X V2) X V3
不过叉积关于向量的加法还是可以分配的:V1 X (V2 + V3)≠(V1 X V2) +(V1 X V3)
点和向量就先复习这些,后面根据需要在补充。
1.3.2.4 点、向量与D3D
我们来把点和向量与D3D联系起来。
在D3D库中,我们可以看到一些用来表示向量的结构体。
如: D3DXVECTOR2 ,D3DXVECTOR3,D3DXVECTOR4
1 typedef struct D3DXVECTOR3 : public D3DVECTOR
2 {
3 public:
4
5 D3DXVECTOR3() {};
6 D3DXVECTOR3( CONST FLOAT * );
7 D3DXVECTOR3( CONST D3DVECTOR& );
8 D3DXVECTOR3( CONST D3DXFLOAT16 * );
9 D3DXVECTOR3( FLOAT x, FLOAT y, FLOAT z );
10
11 // casting 类型转换
12 operator FLOAT* ();
13 operator CONST FLOAT* () const;
14
15 // assignment operators 分配运算符
16 D3DXVECTOR3& operator += ( CONST D3DXVECTOR3& );
17 D3DXVECTOR3& operator -= ( CONST D3DXVECTOR3& );
18 D3DXVECTOR3& operator *= ( FLOAT );
19 D3DXVECTOR3& operator /= ( FLOAT );
20
21 // unary operators 一元运算
22 D3DXVECTOR3 operator + () const;
23 D3DXVECTOR3 operator - () const;
24
25 // binary operators 二元运算
26 D3DXVECTOR3 operator + ( CONST D3DXVECTOR3& ) const;
27 D3DXVECTOR3 operator - ( CONST D3DXVECTOR3& ) const;
28 D3DXVECTOR3 operator * ( FLOAT ) const;
29 D3DXVECTOR3 operator / ( FLOAT ) const;
30 friend D3DXVECTOR3 operator * ( FLOAT, CONST struct D3DXVECTOR3& );
31 BOOL operator == ( CONST D3DXVECTOR3& ) const;
32 BOOL operator != ( CONST D3DXVECTOR3& ) const;
33
34 } D3DXVECTOR3, *LPD3DXVECTOR3;
35
36 //D3DXVECTOR3是从D3DVECTOR继承的
37
38 typedef struct _D3DVECTOR {
39 float x, y, z;
40 } D3DVECTOR;
41
42
1
6
7
8 // 计算向量大小:
9
10 FLOAT D3DXVec3Length( // Returns the magnitude.返回大小
11 CONST D3DXVECTOR3* pV // The vector to compute the length of. 计算向量长度
12 );
13 D3DXVECTOR3 v(1.0f, 2.0f, 3.0f);
14 float magnitude = D3DXVec3Length( &v ); // = sqrt(14)
15
16
17
18 // 规范(单位)化向量:
19
20 D3DXVECTOR3 *D3DXVec3Normalize(
21 D3DXVECTOR3* pOut, // Result.
22 CONST D3DXVECTOR3* pV // The vector to normalize.
23 );
24
25
26
27 // 向量加、减法:
28
29 D3DXVECTOR3 u(2.0f, 0.0f, 1.0f);
30 D3DXVECTOR3 v(0.0f, -1.0f, 5.0f);
31 // (2.0 + 0.0, 0.0 + (-1.0), 1.0 + 5.0)
32 D3DXVECTOR3 sum = u + v; // = (2.0f, -1.0f, 6.0f)
33
34
35 D3DXVECTOR3 u(2.0f, 0.0f, 1.0f);
36 D3DXVECTOR3 v(0.0f, -1.0f, 5.0f);
37 D3DXVECTOR3 difference = u - v; // = (2.0f, 1.0f, -4.0f)
38
39
40
41 // 数乘:
42
43 D3DXVECTOR3 u(1.0f, 1.0f, -1.0f);
44 D3DXVECTOR3 scaledVec = u * 10.0f; // = (10.0f, 10.0f, -10.0f)
45
46
47
48 //标量积(点积、点乘):
49
50 FLOAT D3DXVec3Dot( // Returns the result.
51 CONST D3DXVECTOR3* pV1, // Left sided operand.
52 CONST D3DXVECTOR3* pV2 // Right sided operand.
53 );
54 D3DXVECTOR3 u(1.0f, -1.0f, 0.0f);
55 D3DXVECTOR3 v(3.0f, 2.0f, 1.0f);
56 // 1.0*3.0 + -1.0*2.0 + 0.0*1.0
57 // = 3.0 + -2.0
58 float dot = D3DXVec3Dot( &u, &v ); // = 1.0
59
60
61 // 叉乘:
62
63 D3DXVECTOR3 *D3DXVec3Cross(
64 D3DXVECTOR3* pOut, // Result.
65 CONST D3DXVECTOR3* pV1, // Left sided operand.
66 CONST D3DXVECTOR3* pV2 // Right sided operand.
67 );
68
69
1.3.3 矩阵
若干个量组成的长方形队列就是矩阵。这些量自然就是矩阵的元素。这些量可以是数字、函数、数值表达式等,以行数和列数标识。行列相等的矩阵也叫方阵。如一个m*n的矩阵为:
{a11 a12 ... a1n }
A=| a21 a22 ... a2n |
{am1 am2 ... amn}
ajk的意思是矩阵A的j行,k列元素。也就是说任何元素的第一个下标代表行数,第二个为列数。
矩阵可以认为是行向量或列向量的集合,数学中往往以列矩阵表示向量:
{ Vx }
V=| Vy |
{ Vz }
1.3.3.1 标量乘法和矩阵加法
标量乘法:
若 矩阵A乘以标量S,则:S乘以A中的每一个元素从而得到相乘所得的矩阵。(S*ajx);
矩阵加法:
矩阵加法只有在两个矩阵行数和列数都相等才有意义,运算时各元素对应相加即可。矩阵加法满足分配律。
1.3.3.2 矩阵乘法
矩阵A的列数等于矩阵B的行数时:乘积矩阵C=A的行元素与B的列元素乘积的和
Ex:
{ 0 -1 } {0*1+(-1)*3 0*2+(-1)*4 } { -3 -4 }
| 5 7 | * { 1 2 } = | 5*1+7*3 5*2+7*4 | = | 26 38 |
{-2 8 } { 3 4 } {-2*1+8*3 -2*2+8*4 } { 22 28 }
此外,矩阵乘法并不满足交换律。
1.3.3.3 矩阵转置
矩阵转置由矩阵的行列元素颠倒得到,即:原有的行元素成为列元素;列元素成为行元素。
对于矩阵的积,转置遵循以下规则:(AB)T=BTAT
1.3.3.4 矩阵的秩
对于方阵,可以组合矩阵单元以生成数,称为秩。秩的定义是递归的。
Ex:一个2*2矩阵,二价秩的定义为:
| a11 a12 |
| a21 a22 | = a11*a22-a12*a21
借助较低的秩可以计算较高的秩。计算3价以上的秩的时候可以以n x n矩阵的任意k列,按以下公式计算:
n
det A= ∑ (-1)j+k ajkdetAjk
j=1
detA∫k是从矩阵A删掉第j行和第k列得到的子矩阵.
当计算大矩阵的秩,通常采用数值法。计算秩的一种途径是把矩阵分解成两个因子 A=LU,矩阵L在对角线上的所有元素为0,而矩阵U在对角线以下的所有元素为0 , 计算L和U的积,两积相乘就可以得到detA,该方法是基于秩的如下特征:det(AB)=(detA)(detB)
对于秩不太理解的地方,可以等后面用到时候以实例做参照理解。
1.3.3.5 矩阵的逆矩阵
对于方阵当且仅当矩阵的秩不为0的时候,我们可以得到它的逆矩阵,一个n x n矩阵的逆矩阵记作A-1,且AA-1=A-1A=I
I为单位矩阵,其对角线元素为1,其余为0。
逆矩阵A-1的元素,可以从A的元素计算得来:
ajk-1 ={ (-1)j+k detAjk } / detA
ajk-1是A-1第j行和第k列的单元 , 而Ajk 是从A删去第j行和第k列得到的子矩阵。
来看一个例子:
考虑等式p’= pR 并且假设我们知道p’和R想求p。首先找到R–1,一旦求得R–1,我们便能求出p,就象这样:

由上,简单总结下逆矩阵:
● 只有正方形的矩阵(方阵)才能求逆,因此当我们说矩阵求逆,那么它就是方矩阵。
● n×n矩阵A的逆矩阵是一个n×n矩阵表示为A–1
● 不是每个方矩阵都逆矩阵
● 矩阵和它的逆矩阵相乘得到一个单位矩阵:A A–1 = A–1A = I。注意当我们进行这样的操作时矩阵是可交换的。
1.3.3.6 矩阵与D3D
在D3D中表示1×4的行向量,我们用D3DXVECTOR3和D3DXVECTOR4向量类。当然D3DXVECTOR3只3个成员,不是4个。然而,第4个成员缺省是1或0。
D3D表示4×4矩阵,用D3DXMATRIX类:
1 typedef struct D3DXMATRIX : public D3DMATRIX {
2 public:
3 D3DXMATRIX() {};
4 D3DXMATRIX( CONST FLOAT * );
5 D3DXMATRIX( CONST D3DMATRIX& );
6 D3DXMATRIX( FLOAT _11, FLOAT _12, FLOAT _13, FLOAT _14,
7 FLOAT _21, FLOAT _22, FLOAT _23, FLOAT _24,
8 FLOAT _31, FLOAT _32, FLOAT _33, FLOAT _34,
9 FLOAT _41, FLOAT _42, FLOAT _43, FLOAT _44 );
10 // access grants
11 FLOAT& operator () ( UINT Row, UINT Col );
12 FLOAT operator () ( UINT Row, UINT Col ) const;
13
14 // casting operators
15 operator FLOAT* ();
16 operator CONST FLOAT* () const;
17
18 // assignment operators
19 D3DXMATRIX& operator *= ( CONST D3DXMATRIX& );
20 D3DXMATRIX& operator += ( CONST D3DXMATRIX& );
21 D3DXMATRIX& operator -= ( CONST D3DXMATRIX& );
22 D3DXMATRIX& operator *= ( FLOAT );
23 D3DXMATRIX& operator /= ( FLOAT );
24
25 // unary operators
26 D3DXMATRIX operator + () const;
27 D3DXMATRIX operator - () const;
28
29 // binary operators
30 D3DXMATRIX operator * ( CONST D3DXMATRIX& ) const;
31 D3DXMATRIX operator + ( CONST D3DXMATRIX& ) const;
32 D3DXMATRIX operator - ( CONST D3DXMATRIX& ) const;
33 D3DXMATRIX operator * ( FLOAT ) const;
34 D3DXMATRIX operator / ( FLOAT ) const;
35 friend D3DXMATRIX operator * ( FLOAT, CONST D3DXMATRIX& );
36 BOOL operator == ( CONST D3DXMATRIX& ) const;
37 BOOL operator != ( CONST D3DXMATRIX& ) const;
38 } D3DXMATRIX, *LPD3DXMATRIX;
39
40
41
42
43
44
45 //D3DXMATRIX类是从D3DMATRIX结构继承的:
46
47 typedef struct _D3DMATRIX {
48 union {
49 struct {
50 float _11, _12, _13, _14;
51 float _21, _22, _23, _24;
52 float _31, _32, _33, _34;
53 float _41, _42, _43, _44;
54 };
55 float m[4][4];
56 };
57 } D3DMATRIX;
58
59
D3DXMATRIX类可以发现很多运算符,如检测矩阵相等,相加减,与数相乘,铸造casting,以及非常重要的两个D3DXMATRIXs彼此相乘。
1 D3DXMATRIX A(…); // 初始化矩阵 A
2 D3DXMATRIX B(…); // 初始化矩阵 B
3 D3DXMATRIX C = A * B; // C = AB
D3DXMATRIX类另一个重要的运算符是小括号,它允许我们非常方便的为矩阵成员赋值。当用小括号时下标就象数组下标一样是从0开始的。例如,访问矩阵的第ij = 11 成员:
1 D3DXMATRIX M;
2 M(0, 0) = 5.0f; // 设置入口 ij = 11 to 5.0f.
D3D库也提供了一些函数:如将D3DXMATRIX转化为单位矩阵,转置D3DXMATRIX矩阵及求逆矩阵。
1 D3DXMATRIX *D3DXMatrixIdentity(
2 D3DXMATRIX *pout
3 );
4
5 //参数:
6
7 //pOut 指向D3DXMATRIX结构的返回单位矩阵。
8
9 //返回值:
10
11 //指向D3DXMATRIX 结构的单位矩阵。
12
13 D3DXMATRIX M;
14 D3DXMatrixIdentity( &M ); // M = 单位矩阵
15
16 D3DXMATRIX *D3DXMatrixTranspose(
17 D3DXMATRIX *pOut,
18 CONST D3DXMATRIX *pM
19 );
20
21 //参数:
22 //pOut
23 // 指向D3DXMATRIX 结构的操作结果矩阵。
24 //pM
25 // 指向D3DXMATRIX 结构的源矩阵。
26 //返回值:
27 //指向D3DXMATRIX 结构的转置矩阵。
28
29 //说明:
30 //函数返回值跟pOut 参数返回值是一样的。这样可以让函数D3DXMatrixTranspose作为其它函数的参数使用。
31
32
33 D3DXMATRIX A(...); // initialize A
34 D3DXMATRIX B;
35 D3DXMatrixTranspose( &B, &A ); // B = transpose(A)
36
37 D3DXMATRIX *D3DXMatrixInverse(
38 D3DXMATRIX *pOut,
39 FLOAT *pDeterminant,
40 CONST D3DXMATRIX *pM
41 );
42
43 //参数:
44 //pOut
45 // 指向D3DXMATRIX结构的逆矩阵。
46 //pDeterminant
47 // 指向FLOAT 类型的对角线[1,1][2,2][3,3][4,4]积,如果不需要,可以设置为 NULL。
48 //pM
49 // 指向 D3DXMATRIX 结构源矩阵。
50
51 //返回值:
52 //指向D3DXMATRIX 结构的逆矩阵。如果没有逆矩阵,就返回NULL值。
53 //返回值是跟pOut 参数的返回值是一样的,这样可以让本函数成为其它函数的参数。
54
55
56
57
假如我们将不能求逆的矩阵用求逆函数,那么函数将会返回null.同样的,这本书我们忽视第二个参数,并且总是把它设置为0。
1 D3DXMATRIX A(...); // 初始化 A
2 D3DXMATRIX B;
3 D3DXMatrixInverse( &B, 0, &A ); // B = 逆(A)
1.3.4 复数和四元数
四元数有个别称:最简单的超复数。实际上可以理解为四元数是复数概念的扩展,复数的概念由四元数扩展到高维在抽象代数的发展上有很重要的意义。四元数可以构造强制变换的有力工具,尤其是在物体的旋转和变换中。
先来理解一下复数:
复数由实部和虚部组成:z=(a+b*i) ,其中a为实部,b为虚部。
下面来看下复数的九种运算方式:sqrt(a2+b2)
1.复数的范数:复数向量的模.
2.复数与标量相乘或相除:符合乘法分配律,实部与虚部分别进行乘除运算.
3.复数加法和减法:实部与实部相加减,虚部与虚部相加减。
4.复数加法恒等元:与任何复数相加,结果仍未该复数。(0+0*i),加法恒等元好似实数中0的概念.
5.复数加法逆元素:任何复数与其加法逆元素相加,结果为复数加法恒等元。
6.共轭复数:指两个复数,实部相等,虚部互为相反数,这两个复数互为共轭复数。
7.复数乘法:以一个复数的实部和虚部分别去乘另一个复数的实部和虚部,结果相加。复数相乘得到的是一个新的复数,符合乘法分配律。
8.复数除法:除数和被除数,同时乘以除数的共轭复数,转换为复数除以实数的运算。
9.复数的倒数和复数本身相乘,结果为1。(1+0*i)
与复数相似,一个四元数有一个实部三个虚部:q=s+ia+jb+kc
其中,虚数项系数a.b.c.是实数;参数s也是实数,称为标量部分。而参数i,j,k是虚数:
i2=j2=k2=-1 ij=ji=k (1)
=> jk=-kj=i , ki=-ik=j (2)
i,j,k可以看作3个相互垂直的单位向量,这七个叫做四元数的basis ,向量基。
其标量的乘法为:以四元数的4个分量的每一个分量乘以标量的值,加法也是同样的道理。
两个四元数的乘法遵循 (1)、(2)两个方程式的操作。
四元数的排列法和复数类似:q=(s,v),v是向量(a,b,c)于是:
四元数的加法:q1+q2=(s1+s2,v1+v2)
四元数的乘法:q1*q2=(s1s2-v1●v2, s1v2+s2v1+v1 X v2)
四元数的平方值:|q|2=s2+v v
四元数的逆:q-1=(1/|q|2) * (s,-v)
所以有:qq-1=q-1q=(1,0)
四元数的理解和应用需要一个过程,这里就先复习这些。
1.3.5 图形变换
在复习这部分内容之前,必须明确三维图形变换的显示流程:
输入用户坐标 -> 投影 -> 对窗口裁剪 -> 窗口到视区的变换 -> 显示或绘图
先来看下齐次坐标的内容。
1.3.5.1 齐次坐标
将一个原本是n维的向量用一个n+1维向量来表示,这就是所谓的齐次坐标表示法了。 为实数。显然一个向量的齐次表示是不唯一的,齐次坐标的h取不同的值都表示的是同一个点,比如齐次坐标[8,4,2]、[4,2,1]表示的都是二维点[2,1]。
普通坐标和齐次坐标的关系为宜一对多。若二维点(x,y)的齐次坐标为(hx,hy,h) , 则[h1x, h1y, h1] , [h2x, h2y, h2],.....等等 ,而它们实际上都表示二维空间中的同一个点 (x , y) 的齐次坐标 , 就好像[8,4,2]、[4,2,1]。同理:三维空间的齐次坐标为[hx,hy,hz,h]。那如此煞费波折的使用它是为了什么呢?
首先,提供了以矩阵运算把二维,三维甚至高维空间中的一个点集从一个坐标系变换到另一个坐标系的有效方法。
一个二维的齐次坐标变换矩阵的形式是一个三维的方形矩阵。
a d g
A = { b e h }
c f i
其次,可以表示一个无穷远的点。如:n+1维中, h=0的齐次坐标实际上标识了一个n维的无穷远点。
对于二维齐次坐标[a, b, h]: 当h->0, 表示了ax+by=0的直线 , 即: 在 y= -(a/b)x 上的连续点 [x, y], 逐渐趋于无穷远, 但斜率不变. 那在三维情况下利用其次坐标表示视点在原点时的投影变换 , 几何意义上便会更加清晰了.
一个齐次向量可以表示为 : p=(px , py , pz , pw) , 对于点, pw=1 ;对于向量, pw=0. 而如果是投影变换可以用其他值来取代pw , 得到的是经过投影的点。
1.3.5.2 二维图形几何变换
总纲:
如果:
a d g
A = { b e h }
c f i
那么:
a,b,d,e,完成对图形的缩放, 旋转, 对称, 错切等变换.
c, f : 平移变换
g, h: 投影变换
其中, g可在y轴的1/g处产生一个灭点 ; h可在 y轴的1/h 处产生一个灭点 .
i : 可对整个图形伸缩变换.
平移变换:
1 0 0
[x" y" 1]= [x y 1] * [0 1 0]=[x+Tx y+Ty 1]
Tx Ty 1
比例变换(缩放变换, 下同):
Sx 0 0
[x" y" 1]= [x y 1] * [ 0 Sy 0]=[Sx*x S y*y 1]
0 0 1
Sx=Sy=1时: 恒等比例变换;
Sx=Sy>1时: 等比例放大;
Sx=Sy<1时: 等比例缩小;
Sx不等于Sy时: 非均匀变换
对称变换:
a d 0
[x" y" 1]= [x y 1] * [b e 0]=[ax+by x+ey 1]
0 0 1
旋转变换:
cosθ sinθ 0
[x" y" 1]= [x y 1] * [-sinθ cosθ 0]=[xcosθ-ysinθ xsinθ+yxcosθ 1]
0 0 1
错切变换:
1 d 0
[x" y" 1]= [x y 1] * [b 1 0]=[x+by dx+y 1]
0 0 1
上面这些如果想通了, 复合变换其实也就无需多说了 , 其实我们主要明白的是原理, 大部分时候, 我们还是使用数学库来运算的 :)
1.3.5.3 三维图形几何变换
1.3.5.3.1 基本变换
其实看完上面的二维变换, 三维也就好理解多了.
总纲:
变换矩阵
三维图形的几何变换通过一个4*4的矩阵来表示:
a11 a12 a13 a14
T= { a21 a22 a23 a24 }
a31 a32 a33 a34
a41 a42 a43 a44
变换的功能以4个子矩阵来体现:
a11,a12.a13;a21,a22,a23;a31,a32,a33 : 也就是一个3*3的矩阵 , 负责 比例, 旋转 , 错切 等变换;
a41,a42,a43: 平移变换 ;
a14,a24,a34: 投影变换;
a44 : 整体比例变换.
(1)平移变换
1 0 0 0
0 1 0 0
[x" y" z" 1]=[x y z 1]=[0 0 1 0 ] =[x+Tx y+Ty z+Tz 1]
Tx Ty Tz 1
(2)比例变换
矩阵S(s)=S(sx,sy,sz). 使对象沿xyz轴以缩放因子sx,sy,sz放大或缩小, 值越大, 倍数越大, 若各分量为1 , 则表示没有缩放.
sx 0 0 0
S(s)= { 0 sy 0 0 }
0 0 sz 0
0 0 0 1
缩放因子的一个或者三个分量如果置负, 就会产生一个 Reflective Matrix (反射矩阵) , 也称为iMirror Matrix (镜像矩阵) .如其中两个因子是-1将会旋转180度 . 当发现变换矩阵为反射矩阵的时候, 通常需要特殊处理.
缩放矩阵S(s)的逆矩阵为: S"(s)=S(1/sx , 1/sy, 1/sz)
(3)旋转变换
我们以矩阵R来表示一个旋转矩阵, 同样的三维环境下, 它是4*4的矩阵 , 如果是二维则是3*3矩阵.
假设: Rx(θ) , Ry(θ) , Rz(θ) , 分别为:绕x , y , z轴的旋转变换 , 旋转角度为θ , 则各旋转矩阵表示为:
1 0 0 0
Rx(θ) ={ 0 cosθ sinθ 0 }
0 -sinθ cosθ 0
0 0 0 1
cosθ 0 -sinθ 0
Ry(θ) ={ 0 1 0 0 }
sinθ 0 cosθ 0
0 0 0 1
cosθ sinθ 0 0
Rz(θ) ={ -sinθ cosθ 0 0 }
0 0 1 0
0 0 0 1
假设点 P(px, py, pz, 1) , 则p 与Rz(θ)的乘积为 :
cosθ sinθ 0 0
pR= (px, py, pz, 1) { -sinθ cosθ 0 0 } = (pxcosθ-pysinθ, pxsinθ+pycosθ, pz ,1) 得到一个变换后的新点 p"
0 0 1 0
0 0 0 1
对于绕任意轴旋转角度θ的旋转矩阵R , 从中取出与旋转变换相关的3*3的子矩阵, 可以计算出其对角元素之和 是一个与坐标轴勿怪的常数, 称为: Trace (迹)
tr(R)=1+2cosθ
所以旋转矩阵R, 可以旋转的同时保持各点的位置.
1.3.5.3.2 特殊变换
(1)欧拉变换
通常用于构造一个自定位或使任何实体处于特定方向的矩阵.
首先, 定义一个默认的观察方向, 欧拉变换是绕三个旋转轴的旋转矩阵的乘积 : M=Rx Ry Rz
三个坐标轴的旋转角度成为欧拉角Euler. 绕x轴的是倾斜角pitch, y轴的是 翻滚角或偏转角 head or yaw ,z轴为摇摆角 roll, 物体朝向以欧拉角表示。但需要注意的是:
1.它的旋转必须按某个特定次序进行.
2.有可能导致 Gimbal Lock 顾名思义, 万向节死锁. example:一个平行与学】轴的向量绕y轴旋转90度,平行于x轴,那么所有绕z轴的旋转都不再起作用。
(1)四元数变换
为了解决欧拉变化中的死锁问题,可以引入四元数变换。它占用的空间较小,当然,如果矩阵相乘采用了硬件实现,那么,矩阵乘法,效率将更高。由于有了它就不需要计算三角函数,所以转换过程效率较高。这里需要提及矩阵和四元数之间的相互转换,本文此处暂且不提。
1.3.5.3.3 投影变换
投影是什么? (x, y, z) => (x, y) ,n 维空间的点变换为小于n维空间的点. 投影,主要包括三个方面 投影的对象; 投影的面 和投影线,投影线是投影对象与投影面之间的联线.以投影线的角度分: 主要分为 平行投影和透视投影.(Parallel Projection & Perspective Projection).
平行投影里面有正交平行投影和斜交平行投影.
所谓正交平行投影, 投影线与投影面成90度角,所以,如果投影到x,y平面.则投影对象的x,y分量不变,z分量变为0.斜交平行投影是投影线与投影面成α角.交点a离开正交投影与投影面的交点b的距离为L, L与X夹角为Φ则: x"=x+LcosΦ ,y"=x+YsinΦ , z"=0.其中 L与α的关系: tanα=z/L. 所以α一定时Lz成正比.如果z=1, 它的矩阵运算为 a11, a22, a44.为1 . a31,a32为L1cosΦ.L1sinΦ.其他为0.
透视投影是一组从投影中心产生的不平行的投影线. 不平行于投影平面的视线汇聚的一点称为灭点.,也就是投影中心.在坐标轴上的灭点叫做主灭点, 按照主灭点的个数可分为一点透视和二点、三点透视.一般情况,只考虑一点透视.
为简化问题的叙述,导出视点选在z轴上,且取与此轴垂直的坐标平面为画面的透视投影公式。设视点E(0,0,ze)在z轴上,空间点为P(xp,yp,zp),则视线EP的直线方程为:

透视投影转换为平行投影,遵循:对一个空间物体,一定存在另一个空间物体,使前者在画面上的透视投影与后者的平行投影是一样的,且保留了深度方向的对应关系。