有一个水缸点漏水(而且漏水的速度还不一定固定不变),要求水面高度维持在某个位置,一旦发现水面高度低于要求位置,就要往水缸里加水。
小明接到任务后就一直守在水缸旁边,时间长就觉得无聊,就跑到房里看小说了,每30分钟来检查一次水面高度。水漏得太快,
每次小明来检查时,水都快漏完了,离要求的高度相差很远,小明改为每3分钟来检查一次,结果每次来水都没怎么漏,不需要加水,来得太频繁做的是无用功。
几次试验后,确定每10分钟来检查一次。这个检查时间就称为采样周期。
开始小明用瓢加水,水龙头离水缸有十几米的距离,经常要跑好几趟才加够水,于是小明又改为用桶加,一加就是一桶,跑的次数少了,加水的速度也快了,
但好几次将缸给加溢出了,不小心弄湿了几次鞋,小明又动脑筋,我不用瓢也不用桶,老子用盆,几次下来,
发现刚刚好,不用跑太多次,也不会让水溢出。这个加水工具的大小就称为比例系数。
小明又发现水虽然不会加过量溢出了,有时会高过要求位置比较多,还是有打湿鞋的危险。他又想了个办法,在水缸上装一个漏斗,
每次加水不直接倒进水缸,而是倒进漏斗让它慢慢加。这样溢出的问题解决了,但加水的速度又慢了,有时还赶不上漏水的速度。
于是他试着变换不同大小口径的漏斗来控制加水的速度,最后终于找到了满意的漏斗。漏斗的时间就称为积分时间 。
小明终于喘了一口,但任务的要求突然严了,水位控制的及时性要求大大提高,一旦水位过低,必须立即将水加到要求位置,而且不能高出太多,否则不给工钱。
小明又为难了!于是他又开努脑筋,终于让它想到一个办法,常放一盆备用水在旁边,一发现水位低了,不经过漏斗就是一盆水下去,这样及时性是保证了,但水位有时会高多了。
他又在要求水面位置上面一点将水凿一孔,再接一根管子到下面的备用桶里这样多出的水会从上面的孔里漏出来。这个水漏出的快慢就称为微分时间。
拿一个水池水位来说,我们 可以制定一个规则,
把水位分为超高、高、较高、中、较低、低、超低几个区段;
再把水位波动的趋势分为甚快、快、较快、慢、停几个区段,并区分趋势的正负;
把输出分为超大幅 度、大幅度、较大幅度、微小几个区段。
当水位处于中值、趋势处于停顿的时候,不调节;
当水位处于中值、趋势缓慢变化的时候,也可以暂不调节;
当水位处于较高、趋势缓慢变化 的时候,输出一个微小调节两就够了;
当水位处于中值、趋势较快变化的时候,输出进行叫 大幅度调节……。
如上所述,我们需要制定一个控制规则表,然后制定参数判断水位区段的界值、波动趋 势的界值、输出幅度的界值。
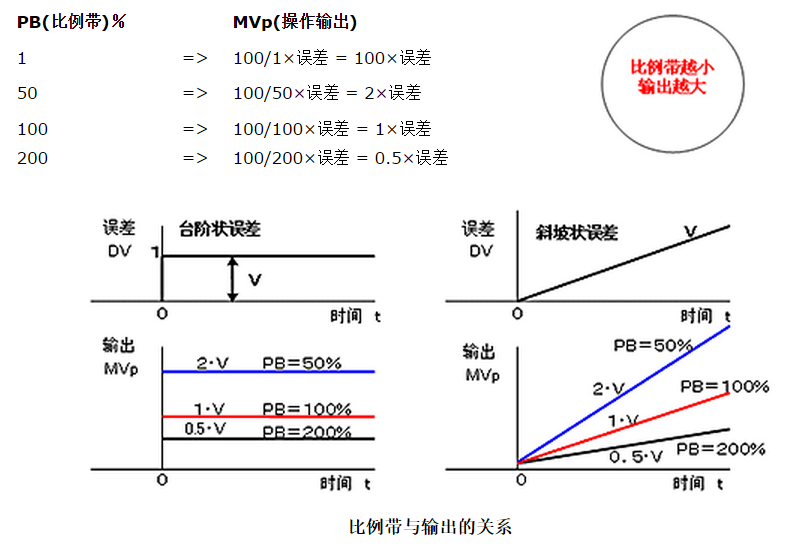
比例控制(P)是一种最简单的控制方式。其控制器的输出与输入误差信号成比例关系。
根据设备有所不同,比例带一般为2~10%(温度控制)。
但是,仅仅是P控制的话,会产生下面将提到的offset (稳态误差),所以一般加上积分控制(I),以消除稳态误差。
比例带与比例控制(P)输出的关系如图所示。用MVp运算式的设定举例:
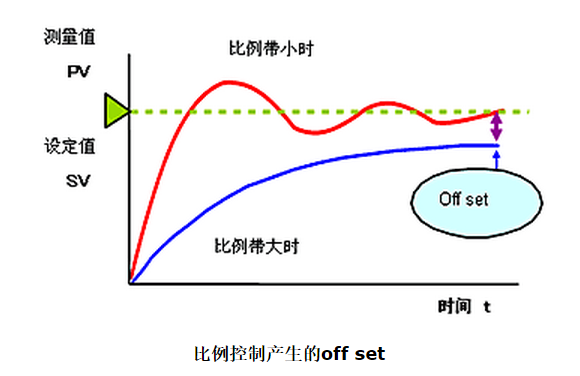
稳态误差(Off set)
比例控制中,经过一定时间后误差稳定在一定值时,此时的误差叫做稳态误差(off set)。
仅用比例控制的时候,根据负载的变动及设备的固有特性不同,会出现不同的稳态误差。
负载特性与控制特性曲线的交点和设定值不一致是产生稳态误差的原因。
比例带小时不会产生。为消除稳态误差,我们设定手动复位值--manual reset值(MR),以消除控制误差。
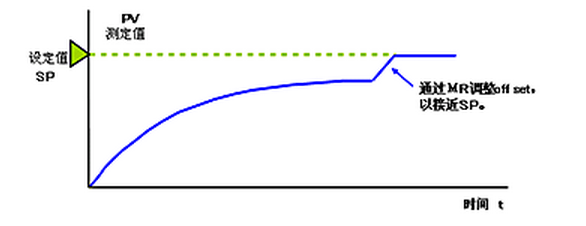
手动复位(Manual reset)
如前所述,仅用比例控制不能消除稳态误差。
为此,将MR(manual reset值)设为可变,则可自由整定(即调整)调节器的输出。
只要手动操作输出相当于offset的量,就能与目标值一致。
这就叫做手动复位(manual reset),通常比例调节器上配有此功能。
在实际的自动控制中,每次发生off set时以手动进行reset的话,这样并不实用。
在后面将叙述的积分控制功能,能自动消除稳态误差。
所谓积分控制(I),就是在出现稳态误差时自动的改变输出量,使其与手动复位动作的输出量相同,达到消除稳态误差的目的。
当系统存在误差时,进行积分控制,根据积分时间的大小调节器的输出会以一定的速度变化,只要误差还存在,就会不断的进行输出。
积分时间的定义:
当积分项和比例项对于控制器的输出的贡献相同,即积分作用重复了一次比例作用时所花费的时间,就是积分时间。

微分控制(D)的功能是通过误差的变化率预报误差信号的未来变化趋势。
通过提供超前控制作用,微分控制能使被控过程趋于稳定。
因此,它经常用来抵消积分控制产生的不稳定趋势。

微分时间的定义:
当输入量持续的以一定速率变化时,微分项和比例项对于控制器的输出的贡献相同,
即微分作用重复了一次比例作用时所花费的时间,就是微分时间。
大学时代做机器人时用的PID算法源代码:
#define PID_Uint struct pid_uint
PID_Uint
{
int U_kk;
int ekk;
int ekkk;
int Ur; //限幅输出值,需初始化
int Un; //不灵敏区
//int multiple; //PID系数的放大倍数,用整形数据的情况下,提高PID参数的设置精度 固定为256
int Kp; //比例,从小往大调
int Ti; //积分,从大往小调
int Td; //微分,用巡线板时设为0
int k1; //
int k2;
int k3;
};
/********************************************************************
函 数 名:void Init_PID_uint(PID_uint *p)
功 能:初始化PID参数
说 明:调用本函数之前,应该先对Kp,Ti,Td做设置 ,简化了公式
入口参数:PID单元的参数结构体 地址
返 回 值:无
***********************************************************************/
void Init_PID_uint(PID_Uint *p)
{
p->k1=(p->Kp)+(p->Kp)*1024/(p->Ti)+(p->Kp)*(p->Td)/1024;
p->k2=(p->Kp)+2*(p->Kp)*(p->Td)/1024;
p->k3=(p->Kp)*(p->Td)/1024;
}
/********************************************************************
函 数 名:void reset_Uk(PID_Uint *p)
功 能:初始化U_kk,ekk,ekkk
说 明:在初始化时调用,改变PID参数时有可能需要调用
入口参数:PID单元的参数结构体 地址
返 回 值:无
***********************************************************************/
void reset_Uk(PID_Uint *p)
{
p->U_kk=0;
p->ekk=0;
p->ekkk=0;
}
/********************************************************************
函 数 名:int PID_commen(int set,int jiance,PID_Uint *p)
功 能:通用PID函数
说 明:求任意单个PID的控制量
入口参数:期望值,实测值,PID单元结构体
返 回 值:PID控制量
***********************************************************************/
int PID_common(int set,int jiance,PID_Uint *p)
{
int ek,U_k=0;
ek=jiance-set;
if((ek>(p->Un))||(ek<-(p->Un))) //积分不灵敏区
U_k=(p->U_kk)+(p->k1)*ek-(p->k2)*(p->ekk)+(p->k3)*(p->ekkk);
p->U_kk=U_k;
p->ekkk=p->ekk;
p->ekk=ek;
if(U_k>(p->Ur)) //限制最大输出量,
U_k=p->Ur;
if(U_k<-(p->Ur))
U_k=-(p->Ur);
return U_k/1024;
}
阅读(7413) | 评论(0) | 转发(0) |