分类:
2011-02-11 15:39:14

在欧几里得几何空间里,两条平行线永远都不会相交。但是在投影空间中,如右图中的两条铁轨在地平线处却是会相交的,因为在无限远处它们看起来相交于一点。
在欧几里得(或称笛卡尔)空间里描述2D/3D 几何物体是很理想的,但在投影空间里面却并不见得。 我们用 (x, y) 表示笛卡尔空间中的一个 2D 点,而处于无限远处的点 (∞,∞) 在笛卡尔空间里是没有意义的。投影空间里的两条平行线会在无限远处相交于一点,但笛卡尔空间里面无法搞定这个问题(因为无限远处的点在笛卡尔空间里是没有意义的),因此数学家想出齐次坐标这个点子来了。
由 August Ferdinand Möbius 提出的齐次坐标(Homogeneous coordinates)让我们能够在投影空间里进行图像和几何处理,齐次坐标用 N + 1个分量来描述 N 维坐标。比如,2D 齐次坐标是在笛卡尔坐标(X, Y)的基础上增加一个新分量 w,变成(x, y, w),其中笛卡尔坐标系中的大X,Y 与齐次坐标中的小x,y有如下对应关系:
X = x/w
Y = y/w
笛卡尔坐标中的点 (1, 2) 在齐次坐标中就是 (1, 2, 1) 。如果这点移动到无限远(∞,∞)处,在齐次坐标中就是 (1, 2, 0) ,这样我们就避免了用没意义的"∞" 来描述无限远处的点。
前面提到,我们分别用齐次坐标中的 x 和 y 除以 w 就得到笛卡尔坐标中的 x 和 x,如图所示:
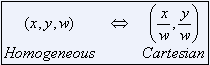
仔细观察下面的转换例子,可以发现些有趣的东西:
上图中,点 (1, 2, 3), (2, 4, 6) 和 (4, 8, 12) 对应笛卡尔坐标中的同一点 (1/3, 2/3)。 任意数量积的(1a, 2a, 3a) 始终对应于笛卡尔坐标中的同一点 (1/3, 2/3)。因此这些点是“齐次”的,因为他们始终对应于笛卡尔坐标中的同一点。换句话说,齐次坐标描述缩放不变性(scale invariant)。
笛卡尔坐标系中,对于如下两个直线方程:
![]()
如果 C ≠ D,以上方程组无解;如果 C = D,那这两条线就是同一条线了。
下面我们用 x/w, y/w 代替 x, y 放到投影空间里来求解:
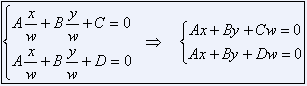
现在我们就可以在 C ≠ D 的情况得到一组解 (x, y, 0),代入得 (C - D)w = 0,因为 C ≠ D,所以 w = 0。因而,两条平行线相交于投影空间中无限远处的一点 (x, y, 0)。
齐次坐标在计算机图形学中是有用的,将 3D 场景投影到 2D 平面的过程中就用到它了。