pku3597 Polygon Division (动态规划)

题目:

题目是上次北大的校赛题，给定一个正多边形，求划分成最小单位为三角形或四边形的种数。例如：正五边形的划分如下，共十种：

现在给出多边形的边数，求出其划分总数。

分析(参考解题报告):如果分出的全为三角形的话，那就是正多边形三角剖分问题。它的结果就是Catalan数。现在也可以划分出四边形的话，可以采用动态规划策略。具体如下：

将n边形的顶点按顺时针或逆时针编号为1,2,3....n(n>=3),设T(n)为最终的结果,E(i,j)为i号顶点和j号顶点连成的对角线(1<=i

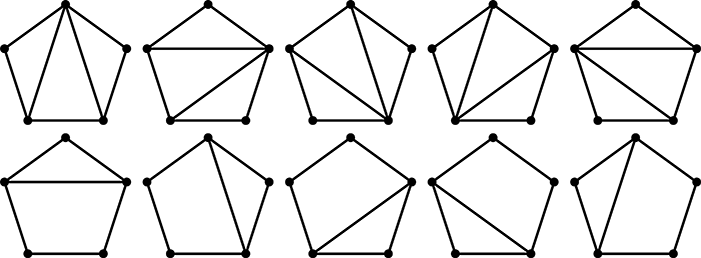
(1)边E(1,n)为划分后一个三角形的一条边。i为该三角形的另外一个顶点(2<=i<=n-1),因此，对角线E(1,i)和对角线E(i,n)将n边形分为1个i边形,1个由顶点(1,i,n)组成的三角形,1个(n-i+1)边形;这种情况下，问题规模缩小为小i边形，和(n-i+1)边形的。此时的种数为:

                 a=∑T(i)*T(n-i+1)   (2<=i<=n-1)

(2)边E(1,n)为划分后一个四边形的一条边。i,j为该四边形的另外两个顶点(2<=i<=n-2,i+1<=j<=n-1)。1,n,i,j四个顶点将n边形分为1个i边形,1个j-i+1边形，1个n-j+1边形和该四边形。我们可以继续将i边形,j-i+1,n-j+1边形继续划分，规模也将继续缩小。此时的种数为：

                 b=∑∑T(i)*T(j-i+1)*T(n-j+1); (2<=i<=n-2,i+1<=j<=n-1)

故T(n)=a+b=∑T(i)*T(n-i+1)+∑∑T(i)*T(j-i+1)*T(n-j+1);

此时的时间复杂度为O(n^3),会TLE,我们可以将上述表达式写成以下形式以降低时间复杂度 

                 U(n)=∑T(i)*T(n-i+1);(2<=i<=n-1)

                 T(n)=U(n)+∑T(i)*U(n-i+1);(2<=i<=n-2)

这样我们可以获得O(n^2).

my code:

 

#include<iostream>
using namespace std;
int main()
{
    unsigned __int64 u[5001],t[5001];
    int i,j,k,n;
    t[2]=1;
    for(k=3;k<=5000;k++)
    {
        u[k]=0;
        for(i=2;i<=k-1;i++)
            u[k]+=t[i]*t[k-i+1];
        t[k]=u[k];
        for(j=2;j<=k-2;j++)
            t[k]+=t[j]*u[k-j+1];
    }
    while(cin>>n)
        printf("%I64u\n",t[n]);
    return 0;
}


这题最后要求结果对2^64取模，我们只要将结果定义为unsigned __int64型，当结果超出2^64时，它会自动取模(摘自discuss).

阅读(1575) | 评论(2) | 转发(0) |

0

上一篇：pku3192 DNA Assembly (暴力)

下一篇：人生戒律