Dijkstra算法

Dijkstra算法

Posted on 2009-07-09 17:19 YDN 阅读(510) 评论(0)  编辑 收藏 网摘 所属分类: 树和图, 贪心

      Dijkstra算法又称为单源最短路径，所谓单源是在一个有向图中，从一个顶点出发，求该顶点至所有可到达顶点的最短路径问题。 
      设G=（V，E）是一个有向图，V表示顶点，E表示边。它的每一条边（i，j）属于E，都有一个非负权W（I,j），在G中指定一个结点v0，要求把从v0到G的每一个接vj（vj属于V）的最短有向路径找出来（或者指出不存在）。
      Dijstra算法是运用贪心的策略，从源点开始，不断地通过相联通的点找出到其他点的最短距离
基本思想是：
      设置一个顶点的集合s，并不断地扩充这个集合，一个顶点属于集合s当且仅当从源点到该点的路径已求出。开始时s中仅有源点，并且调整非s中点的最短路径长度，找当前最短路径点，将其加入到集合s，直到终点在s中。
基本步骤：
1、把所有结点分成两组：
      第一组：包括已经确定最短路径的结点；
      第二组：包括尚未确定最短路径的结点。
2、开始时，第一组只包含起点，第二组包含剩余的点；
3、用贪心的策略，按最短路径长度递增的顺序把第二组的结点加到第一组去，直到v0可达的所有结点都包含于第一组中。在这个过程中，不断更新最短路径，总保持从v0到第一组各结点的最短路径长度dist都不大于从v0到第二组任何结点的路径长度。
4、每个结点对应一个距离值，第一组结点对应的距离就是v0到此结点的最短路径长度，第二组结点对应的距离值就是v0由第一组结点到此结点的最短路径长度。
5、直到所有的顶点都扫描完毕（v0可达的所有结点都包含于第一组中），找到v0到其它各点的所有最短路径。

 动画演示：

 如图：求0点到其他点的最短路径。

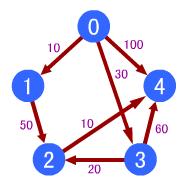
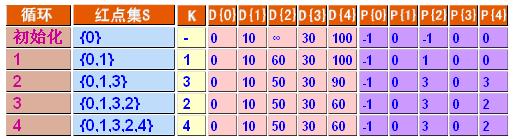
(1)开始时，s1={v0},s2={v1,v2,v3,v4}，v0到各点的最短路径是{0,10,&,30,100};
(2)在还未进入s1的顶点之中，最短路径为v1，因此s1={v0,v1},由于v1到v2有路径，因此v0到各点的最短路径更新为{0,10,60,30,100};
(3)在还未进入s1的顶点之中，最短路径为v3，因此s1={v0,v1,v3},由于v3到v2、v4有路径，因此v0到各点的最短路径更新为{0,10,50,30,90}；
(4)在还未进入s1的顶点之中，最短路径为v2，因此s1={v0,v1,v3,v2},由于v2到v4有路径，因此v0到各点的最短路径更新为{0,10,50,30,60};
数据结构：
(1)用一个二维数组a[i..j,i..j]来存储各点之间的距离，10000表示无通路：
(2)用数组dist[i..j]表示最短路径；
(3)用集合s表示找到最短路径的结点。 

Code
 1//单源最短路（dijkstra算法）
 2program dijkstra;
 3const max=10000;    //表示无通路
 4type jihe=set of 0..100;  //顶点数
 5var
 6   a:array[0..100,0..100] of integer;//各点之间的距离
 7   dist:array[0..100] of integer; //最短路径
 8   i,j,k,m,n:integer;
 9   s:jihe;
10
11procedure init;
12begin
13   s:=[0];    //开始集合只包含源点
14   readln(n);
15   assign(input,'dijs.in');reset(input);
16   for i:=0 to n do    //读入各点之间的距离
17      for j:=0 to n do
18         read(a[i,j]);
19   for i:=0 to n do    //源点到各点之间的直接距离
20      dist[i]:=a[0,i];
21end;
22
23procedure dijsk;
24begin
25   for i:=0 to n do
26   begin
27      m:=0;
28      dist[m]:=max;  //初始化源点到各点的最小距离为无穷
29      for j:=1 to n do
30         if(not(j in s))and(dist[m]>dist[j]) then  //找出当前的最小距离
31        m:=j;    //记录找到的顶点    
32         s:=s+[m]; //把顶点加入集合
33      for k:=0 to n do    //更新经过新节点到其它点之间的最小距离
34         if(not(k in s))and(dist[k]>dist[m]+a[m,k]) then
35            dist[k]:=dist[m]+a[m,k];
36   end;
37end;
38
39begin
40   init;
41   dijsk;
42   for i:=1 to n do
43      writeln(i,':',dist[i]);
44   close(input);
45end.