分类: 项目管理
2009-11-18 09:21:51
在图论中经常会遇到这样的问题,在一个有向图里,求出任意两个节点之间的最短距离。当节点之间的权值是正值的时候,我们可以采用Dijkstra算法,用贪心策略加于解决。但当节点之间的权值有负数的时候,Dijkstra就行不通了,这里介绍另外一种算法——Floyd最短路径算法。
问题描述:
如果有一个矩阵D=[d(ij)],其中d(ij)>0表示i城市到j城市的距离。若i与j之间无路可通,那么d(ij)就是无穷大。又有d(ii)=0。编写一个程序,通过这个距离矩阵D,把任意两个城市之间的最短路径找出来。
【分析】
如何找出最短路径呢,这里需要用到动态规划的思想,对于任何一个城市而言,i 到 j 的最短距离不外乎存在经过 i 与 j 之间的k和不经过k两种可能,所以可以令k=1,2,3,...,n(n是城市的数目),再检查d(ij)与d(ik)+d(kj)的值;在此d(ik)与d(kj)分别是目前为止所知道的 i 到 k 与 k 到 j 的最短距离,因此d(ik)+d(kj)就是 i 到 j 经过k的最短距离。所以,若有d(ij)>d(ik)+d(kj),就表示从 i 出发经过 k 再到j的距离要比原来的 i 到 j 距离短,自然把i到j的d(ij)重写为d(ik)+d(kj)<这里就是动态规划中的决策>,每当一个k查完了,d(ij)就是目前的 i 到 j 的最短距离。重复这一过程,最后当查完所有的k时,d(ij)里面存放的就是 i 到 j 之间的最短距离了<这就是动态规划中的记忆化搜索>。利用一个三重循环产生一个存储每个结点最短距离的矩阵.
用三个for循环把问题解决了,但是有一个问题需要注意,那就是for循环的嵌套的顺序:我们可能随手就会写出这样的枚举程序,但是仔细考虑的话,会发现是有问题的:
for i:=1 to n do
for j:=1 to n do
for k:=1 to n do
if.....
问题出在我们太早的把i-k-j的距离确定下来了,假设一旦找到了i-p-j最短的距离后,i到j就相当处理完了,以后不会在改变了,一旦以后有使i到j的更短的距离时也不能再去更新了,所以结果一定是不对的。所以应当象下面一样来写程序:
for k:=1 to n do
for i:=1 to n do
for j:=1 to n do
if .....
这样作的意义在于固定了k,把所有i到j而经过k的距离找出来,然后象开头所提到的那样进行比较和重写,因为k是在最外层的,所以会把所有的i到j都处理完后,才会移动到下一个K。
【Floyd算法实例】
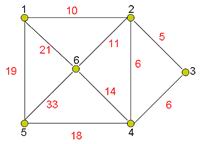
现有一张城市地图,图中的顶点为城市,无向边代表两个城市间的连通关系,边上的权代表城市之间的距离。求每个城市的最短距离
【输入】 第一行两个数v,e,分别代表城市数和边数 以下e行,每行为两个顶点和它们之间的边权。
【输出】 所有可能连接的城市的最短距离。
【输入样例】
6 10
1 2 10
1 5 19
1 6 21
2 3 5
2 4 6
2 6 11
3 4 6
4 5 18
4 6 14
5 6 33
【输出样例】
1 2 10
1 3 15
1 4 16
1 5 19
1 6 21
2 3 5
2 4 6
2 5 24
2 6 11
3 4 6
3 5 24
3 6 16
4 5 18
4 6 14
5 6 32
 program floyd_example;
program floyd_example; const
const maxn=10;
maxn=10; var
var n,s,t,i,j:integer;
n,s,t,i,j:integer; dist:array[1..maxn,1..maxn] of real;
dist:array[1..maxn,1..maxn] of real; prev:array[1..maxn,1..maxn] of 0..maxn;
prev:array[1..maxn,1..maxn] of 0..maxn; procedure init;
procedure init; var
var m,i,u,v:integer;
m,i,u,v:integer; begin
begin assign(input,'floyd.in');
assign(input,'floyd.in'); reset(input);
reset(input); assign(output,'floyd.out');
assign(output,'floyd.out'); rewrite(output);
rewrite(output); readln(n,m);
readln(n,m); fillchar(prev,sizeof(prev),0);
fillchar(prev,sizeof(prev),0); for u:=1 to n do
for u:=1 to n do for v:=1 to n do
for v:=1 to n do dist[u,v]:=1e10;
dist[u,v]:=1e10; for i:=1 to m do
for i:=1 to m do begin
begin readln(u,v,dist[u,v]);
readln(u,v,dist[u,v]); dist[v,u]:=dist[u,v];
dist[v,u]:=dist[u,v]; prev[u,v]:=u;
prev[u,v]:=u; prev[v,u]:=v;
prev[v,u]:=v; end;
end; end;{init}
end;{init} procedure floyd;
procedure floyd; var
var i,j,k:integer;
i,j,k:integer; begin
begin for k:=1 to n do
for k:=1 to n do for i:=1 to n do
for i:=1 to n do for j:=1 to n do
for j:=1 to n do if (dist[i,k]+dist[k,j]<dist[i,j])
if (dist[i,k]+dist[k,j]<dist[i,j])  then begin
then begin dist[i,j]:=dist[i,k]+dist[k,j];
dist[i,j]:=dist[i,k]+dist[k,j]; prev[i,j]:=prev[k,j];
prev[i,j]:=prev[k,j]; end;
end; end;{floyd}
end;{floyd} procedure print(i,j:integer);
procedure print(i,j:integer); begin
begin if i=j
if i=j then write(i)
then write(i) else if prev[i,j]=0
else if prev[i,j]=0 then write('No Solution!')
then write('No Solution!') else begin
else begin print(i,prev[i,j]);
print(i,prev[i,j]); write('->',j);
write('->',j); end;
end; end;{print}
end;{print} begin
begin init;
init; floyd;
floyd; for i:=1 to n do
for i:=1 to n do for j:=i+1 to n do
for j:=i+1 to n do begin
begin write(i,' ',j,' ');
write(i,' ',j,' '); write(dist[i,j]:0:0,' ');
write(dist[i,j]:0:0,' '); print(i,j);
print(i,j); writeln;
writeln; end;
end; close(input);
close(input); close(output);
close(output); end.
end.