hihocode #1141 : 二分·归并排序之逆序对

https://blog.csdn.net/liyi_/article/details/44921521
题目如下：

----------------------------------

Time Limit:10000ms

Case Time Limit:1000ms

Memory Limit:256MB

描述

在上一回、上上回以及上上上回里我们知道Nettle在玩《艦これ》。经过了一番苦战之后，Nettle又获得了的很多很多的船。
这一天Nettle在检查自己的舰队列表：

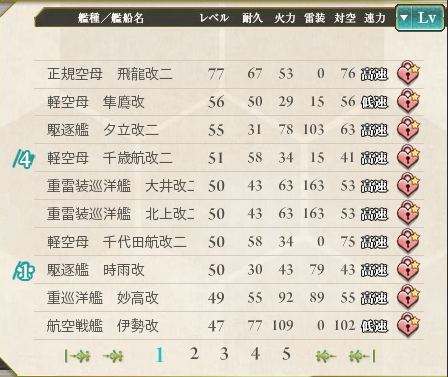
我们可以看到，船默认排序是以等级为参数。但实际上一个船的火力值和等级的关系并不大，所以会存在A船比B船等级高，但是A船火力却低于B船这样的情况。比如上图中77级的飞龙改二火力就小于55级的夕立改二。
现在Nettle将按照等级高低的顺序给出所有船的火力值，请你计算出一共有多少对船满足上面提到的这种情况。

输入

第1行：1个整数N。N表示舰船数量, 1≤N≤100,000
第2行：N个整数，第i个数表示等级第i低的船的火力值a[i]，1≤a[i]≤2^31-1。

输出

第1行：一个整数，表示有多少对船满足“A船比B船等级高，但是A船火力低于B船”。

Sample Input

10
1559614248 709366232 500801802 128741032 1669935692 1993231896 369000208 381379206 962247088 237855491

Sample Output

27

--------------------------------

这题是个典型逆序排队问题，经典解法就是用归并排序来求解。我采用的也是归并的方法，但是在hihocoder提交代码之后，一直提示wrong answer，但是自己用了多组测试用例都没发现有任何问题，简直太郁闷了。。。后来想到那要不用大数据方案测一下呗，于是设置了一个100000大的输入数组，发现返回结果为负数了。。。好，问题来了，返回负值，那不就是存储返回结果的变量不够长吗？真是智商捉急啊！于是将存储返回结果的int型变量变成了long long型的，一下就AC了。回想前几天做的一个微软的笔试题，当时提交答案后也是扣了一半分数，不明原因，现在回想估计有这个原因在里面，回头再去检查一下。

下面简单说一下思路：

在归并排序的过程中，当左右两组（分别长m, n）进行合并时，会临时申请一个m+n长的数组来存两者合并的有序数组。那么当扫面左边和右边数组时，如果发现右边比左边小，那么将右边数组中该元素放入临时数组中。如果发现左边数组大于或者等于右边数组中当前元素，那么将左边数组该元素放入临时数组中，同时更新逆序对的数量，增加的数量等于目前临时数组中的右边数组的元素个数（为什么这么认为呢，因为当前放入的左边数组元素大于临时数组中的所有元素，那么就与临时数组中的所有右边数组的元素构成了逆序对）。没图解释可能比较绕，本博客也只是对本人的一个记录，就将就这么写吧。

代码：

#include <stdio.h>
#include <stdlib.h>

void merge(int *a, int p1, int p2, int p3, long long &sum) {
    if(p2 >= p3) return;

    int leftptr = p1;
    int midptr = p2;
    int *mergetmp = new int[p3-p1];
    int tmpIndex;

    for(tmpIndex = 0; leftptr < p2 && midptr < p3; tmpIndex++) {
        if(a[leftptr] <= a[midptr]) {
            mergetmp[tmpIndex] = a[leftptr];
            sum = sum + tmpIndex-(leftptr-p1);
            leftptr++;
        } else if(a[leftptr] > a[midptr]) {
            mergetmp[tmpIndex] = a[midptr];
            midptr++;
        }
    }
    if(leftptr == p2) { // left segement is shorter than the right
        for(int p=tmpIndex; p<(p3-p1); p++) {
            mergetmp[p] = a[midptr];
            midptr++;
        }
    } else if(midptr == p3) {
        for(int p=tmpIndex; p<(p3-p1); p++) {
            mergetmp[p] = a[leftptr];
            sum = sum + tmpIndex - (leftptr - p1);
            leftptr++;
            tmpIndex++;
        }
    }

    for(int p=0; p<p3-p1; p++) {
        a[p+p1] = mergetmp[p];
    }
    delete mergetmp;
}

int min(int a, int b) {
    return (a < b ? a : b);
}

void merge_c(int *a, int left, int right, int m, long long &sum) {
    if(m >= right - left) return;
    for(int i=0; i<right; i = i+m+m) {
        merge(a, i, i+m, min(i+m+m, right), sum);
    }
    merge_c(a, left, right, m+m, sum);
}

int main(int argc, char *argv[])
{
    int N;
    scanf("%d", &N);
    int *a = new int[N];

    for(int i=0; i<N; i++) {
        scanf("%d", a+i);
    }

    long long sum = 0;
    merge_c(a, 0, N, 1, sum);
    printf("%lld\n", sum);

    return 0;
}

https://blog.csdn.net/Magical_Bubble/article/details/78944854

#include <iostream>
using namespace std;

const int maxn = 1e5 + 50;
int n, A[maxn], larr[maxn], rarr[maxn];

// 寻找[s,e]中有多少逆序对
long long revCnt(int s, int e) {
    long long cnt = 0;
    if (s == e) return cnt;
    int mid = s + (e - s) / 2;
    cnt += revCnt(s, mid) + revCnt(mid+1, e);
    for (int i=s; i<=mid; i++) larr[i] = A[i];
    for (int i=mid+1; i<=e; i++) rarr[i] = A[i];
    int p1 = s, p2 = mid+1, p = s, tmp = 0; // tmp: 存储A中已经有多少个rarr中的元素
    // 每将larr中的元素放入A中时,就统计有多少个rarr的元素已经在A中了,加上即可
    while (p1 <= mid && p2 <= e) {
        if (larr[p1] <= rarr[p2]) A[p++] = larr[p1++], cnt += tmp;
        else A[p++] = rarr[p2++], tmp++;
    }
    while (p1 <= mid) A[p++] = larr[p1++], cnt += tmp;
    while (p2 <= e) A[p++] = rarr[p2++];
    return cnt;
}

int main() {
    // freopen("../input.txt", "r", stdin);
    cin >> n;
    for (int i=0; i<n; i++) cin >> A[i];
    cout << revCnt(0, n-1) << endl;
    return 0;
}

Time -> O(nlogn), Space -> O(n)

这道题目，就是巧妙地利用归并排序中的合并，进行逆序对的个数统计

唯一的坑就在于，最后的结果大小最多为O(n*(n-1)/2)，得用long long存储，不然会发生溢出现象。好几次的WA就是卡在这个地方，还得更加细心啊！！

据说还有一种树状数组的解法，与这个的时间复杂度一致。